Introduction
Forward Error Correction
(FEC) codes can detect and correct a limited number of errors without
retransmitting the data stream. There are two basic types of FEC codes: Block
codes and Convolution codes.
The significant example of
Block code is BCH code. As other block code, BCH encodes k data bits into n
code bits by adding n-k parity checking bits for the purpose of detecting and
checking the errors. Given the
length of the codes is ![]() for any integer
m¡Ý3, we will have t (where t<
for any integer
m¡Ý3, we will have t (where t<![]() ), is the bound of the error correction. That is, BCH can
correct any combination of errors (burst or separate) fewer than t in the
n-bit-codes. The number of parity checking bits is n-k¡Ümt.
), is the bound of the error correction. That is, BCH can
correct any combination of errors (burst or separate) fewer than t in the
n-bit-codes. The number of parity checking bits is n-k¡Ümt.
An important concept for BCH
is Galois Fields (GF), which is a finite set of elements on which two binary
addition and multiplication can be defined. For any prime number p there is GF(p) and GF(![]() is called extended field of GF(p). We often use GF(
is called extended field of GF(p). We often use GF(![]() in BCH code. A GF can be constructed over a primitive
polynomial such as
in BCH code. A GF can be constructed over a primitive
polynomial such as ![]() (The construction and arithmetic of GF are in ¡°Error Control
Coding¡±, by Shu Lin). Usually, GF table records all
the variables, including expressions for the elements, minimal polynomial, and
generator polynomial. By referring to the table, we can locate a proper
generator polynomial for encoder. For example, when (n, k, t)=(15,
7, 2), a possible generator is
(The construction and arithmetic of GF are in ¡°Error Control
Coding¡±, by Shu Lin). Usually, GF table records all
the variables, including expressions for the elements, minimal polynomial, and
generator polynomial. By referring to the table, we can locate a proper
generator polynomial for encoder. For example, when (n, k, t)=(15,
7, 2), a possible generator is ![]() . If we have a data stream
. If we have a data stream![]() , the codeword would be
, the codeword would be ![]() and have the
style of
and have the
style of ![]() .
.
The decoder of BCH is
complicated because it has to locate and correct the errors. Suppose we have a
received codeword![]() , then
, then ![]() , where, v(x) is correct codeword and e(x) is the error.
First, we must compute a syndrome vector s=
, where, v(x) is correct codeword and e(x) is the error.
First, we must compute a syndrome vector s=![]() , which can be achieved by calculating
, which can be achieved by calculating![]() , where, H is parity-check matrix and can be defined as:
, where, H is parity-check matrix and can be defined as:
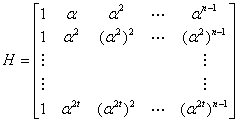 .
.
Here,![]() is the element of the GF field and can be located in the GF
table.
is the element of the GF field and can be located in the GF
table.
With syndrome, error-location
polynomial ![]() can be determined.
Berkekamp¡¯s iterative algorithm is one of solutions
to calculate the error-location polynomial. By finding roots of
can be determined.
Berkekamp¡¯s iterative algorithm is one of solutions
to calculate the error-location polynomial. By finding roots of![]() , the location numbers for the errors will be achieved.
, the location numbers for the errors will be achieved.
Usage
The program is developed with
Java applet. Basically, the implementation involves three steps: Encoder, Error
adding, Decoder.
¡¤
Encoder
m and t are available for adjusting. As mentioned
above, the codeword length will be![]() . t is the bound of error
correction. With m and t being settled, the length of data bits is k=n-mt. Although
the program itself has no boundary for m, considering the display limitation, m
will be set between 3 and 7. The range checking for m and t are available, if m
and t are set to unreasonable values, a red color will be filled input area and
program will keep wait for proper inputs.
. t is the bound of error
correction. With m and t being settled, the length of data bits is k=n-mt. Although
the program itself has no boundary for m, considering the display limitation, m
will be set between 3 and 7. The range checking for m and t are available, if m
and t are set to unreasonable values, a red color will be filled input area and
program will keep wait for proper inputs.
. User will be able to choose either to manually type
data stream in binary (user generate) or allow program to randomly generate
data stream (randomly generate). If ¡°user generate¡± is chosen, user has to type
the data stream, whose length is exact K=n-mt.
Otherwise, when ¡°user gen¡± being click, a range
checking function will fill the input area with red, indicating the data length
is incorrect. If ¡°randomly generate¡± is selected, upon m and t being settled,
the program will randomly generate a data stream and encoder it into codeword.
With
the ¡°random gen¡± or ¡°user gen¡±
button being clicked, the original signal, BCH codeword and its generator
sequence (![]() , It comes from GF and constructs the codeword) will be
displayed. Meanwhile, the data stream and BCH codeword will be show the plot
graph underneath.
, It comes from GF and constructs the codeword) will be
displayed. Meanwhile, the data stream and BCH codeword will be show the plot
graph underneath.
¡¤
Error Adding
In
order to evaluate the capability of BCH codes, user is allowed to decide number
of errors that will happen to codeword. Besides, two error-assignment styles
will be available to be selected:
Random: The faulty bits will be randomly selected from the
codeword;
Burst: The
faulty bits will be consecutive, and user is allowed to set start position for
burst error. In random styles, the start position will be set to ¡°-1¡±, meaning
not available for adjustment. If
the start position that user set exceeds the length of the codeword, the
program will coerce the start position back to signal range. It is well know
that burst errors are hard for normal other error correction codes to deal
with. But user will find burst or separate errors make no difference for BCH
code, which is an advantage of BCH code. When ¡°adding error¡± is clicked, the
receiving code with error bits will be displayed. Meanwhile, corresponding
receiving code will be shown in the plot graph. On the receiving curve, a red
¡°E¡± will appear on the error bit.
¡¤
Decoder
The decoder will be triggered by user clicking the
¡°decode¡±. The decoder will give the results of error corrections, including:
¡¤
decoded signal;
¡¤
sigma(x): ![]() , it is the error-location polynomial and calculated by Berkekamp¡¯s iterative algorithm, which is a quite complex
procedure;
, it is the error-location polynomial and calculated by Berkekamp¡¯s iterative algorithm, which is a quite complex
procedure;
¡¤
root: the roots
for ![]() and they are the
position number of errors;
and they are the
position number of errors;
¡¤
S(x): Syndrome,
which is essential for the decoder (details are discussed above);
¡¤
The number of
corrected errors;
¡¤
The text message,
which indicates whether all the error bits have been corrected.
The
decoded signal will also be shown in the plot graph. If the number of errors
exceeds t, the decoder will fail to correct all the errors. In that case, some
of ¡°E¡±s will be left to indicate that some errors are
still there.
Reference:
[1] Shu
Lin, ¡°Error Control Coding: Fundamentals and Applications¡±,
[2] William
Stallings, ¡°Wireless Communications and Networks¡±, Prentice Hall, 2002.