(1.1)
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
(1.4)
A Comprehensive Kinetic Model for Chlorine Decay and Chlorination Byproduct Formation
John N. McClellan, David A. Reckhow, John E. Tobiason, James K. Edzwald
Department of Civil and Environmental Engineering
University of Massachusetts/Amherst
18 Marston Hall
Amherst, MA 01003
Darrell B. Smith
South Central Connecticut Regional Water Authority
90 Sargent Drive
New Haven, CT 06511
Introduction
Most U.S. water utilities use chlorine to comply with CT requirements, and it is general practice to maintain a low-concentration chlorine residual in water distribution systems. This provides essential public health protection by preventing communication of waterborne infectious disease. Chlorine is a strong oxidant that reacts with the natural organic matter (NOM) present in all natural waters. Although chlorine is invaluable in the protection of public health against waterborne disease, some byproducts of the reactions between chlorine and NOM may represent long-term health risks to water consumers. The trihalomethanes (THMs) and haloacetic acids (HAAs) are two important classes of potentially harmful chlorination byproducts that are currently regulated by the USEPA, and therefore of particular interest to water utilities.
Water suppliers that practice chlorine disinfection face conflicting objectives in providing adequate microbial protection while minimizing the formation of harmful chlorinated organic byproducts. Chlorine/NOM reactions may proceed over a period of days under conditions typical in water distribution systems and variations in the source water quality and in environmental conditions such as temperature and pH can affect the rates and extents of byproduct-forming reactions. As a result of chemical and hydraulic dynamics, the chemical composition of water can vary substantially in time and space in distribution systems. Models that can capture these dynamics would be powerful tools for optimizing water quality in distribution systems.
Mechanistic models are expected to be more robust and flexible than purely empirical models. Mechanistic models may also provide insights into the processes being modeled. It is therefore desirable for kinetic models to reflect the underlying chemistry to the extent possible. Mechanistic modeling has been considered impractical due to the complexity of NOM molecules and NOM/chlorine reaction pathways. However, very complex computations have become feasible using personal computers due to recent advances in computer technology, so that more complex models are practical. The goal of this research is to develop a kinetic model that captures the important mechanistic features of chlorine/NOM reactions.
Background
Existing models. Efforts to model chlorine decay in natural waters began before 1950 (1,2) and a number of studies have been conducted where chlorine decay was modeled in the contexts of drinking water, waste water, and power plant cooling water. The most widely used form for modeling chlorine decay has been the first-order (exponential decay) form. Several investigators have presented empirical models for THM formation as a function of other parameters such as UV absorbance, TOC, pH, temperature and bromide concentration (3-7). These are linear models (in log-transformed variables) that have been fit to large experimental data sets by multivariate linear regression procedures. This approach has also been used to model HAA formation (7). Models that include second-order terms (i.e. terms for both NOM site and chlorine concentration) have been proposed by MacNiell (8), Jedas-Hecart et al. (9), and Clark (10, 11).
Vasconcelos et al. (12) compared several models by fitting them to data sets from bottle tests of eleven different treated waters. Goodness of fit (as measured by the adjusted coefficient of determination R2) for the widely used first-order model was generally poor. For other models compared by Vasconcelos et al. (12), reasonably good fits were achieved with wide variations in the parameter values for the various data sets. This lack of robustness of model parameters is a shortcoming of existing models that we hope to improve with a more mechanistic modeling approach. A mechanistic approach where reactant concentrations and important environmental variables are represented explicitly should be well suited for practical applications such "what if" modeling, modeling of "reactive" chlorination byproducts, and modeling distribution systems with multiple sources of different NOM quality or different chlorine doses.
Reaction mechanisms. The aqueous chlorination of organic compounds has been studied by a number of researchers (13-22). The organic substrates investigated included various pure ketones, organic acids, and aromatics as well as organic fractions extracted from natural waters. Some key findings that bear on the development of a mechanistic model are summarized in this section.
Under conditions typical in water treatment, HOCl and OCl- predominate and Cl2 is not present in significant concentrations. HOCl is expected to be more reactive as an oxidant and halogenating agent than OCl- (23). The functional groups within NOM molecules that have been implicated as important chlorine consumers and byproduct precursors include activated aromatics (particularly those with meta hydroxyl substituents) and some oxygen-rich ketones and keto-acids (16-21). For several ketones and keto-acids, the rate of reaction with halogens is first-order in ketone and not sensitive to halogen concentration except at very low levels (13-15). The reason is a rate-limiting initial dissociation of a proton to form enolate, the reactive species. In the classic haloform reaction of halogens with methyl ketones, enolate formation is followed by a faster halogen addition. After the initial halogenation the remaining protons are more acidic so that the second and third ionizations and halogenations proceed rapidly followed by base-catalyzed hydrolysis to form haloform (23).
For orcinol and resorcinol, the O-substituted species react much faster with chlorine than the corresponding OH substituted species. Nevertheless, the completely protonated species are predominant and are expected to be the most significant participants in chlorine reactions over the pH range of interest in water treatment (22). Acid-base chemistry would play a more important role for aromatics with more acidic substituents, and a first-order rate-limiting step similar to the rate-limiting step of the haloform reaction could be envisioned.
Most of the reaction mechanisms that have been proposed for chloroform formation pass through a trichloromethyl ketone intermediate (16, 19, 21). Chlorine concentration and pH can affect the speciation of products even where reactions of the intermediate are not rate-limiting steps in the overall reaction (21, 24).
The objective is to capture the most important elements of the reaction, i.e. the elements that control the overall reaction rate, and those that affect the proportions of products that are formed. Based on the reaction mechanisms that have been proposed, it seems appropriate to include two conceptual reaction pathways in the model: one with second-order kinetics, and one with a rate-limiting first-order step similar to the haloform reaction. Chlorine consumption and byproduct formation rates will be determined as functions of the reaction rates through these conceptual pathways.
Experimental
A series of bench-scale experiments was conducted to characterize the effects of temperature, pH, and reactant concentrations on chlorine decay and byproduct formation in a treated water. These experiments were conducted using three samples collected at different times from the same source, filter effluent of the Lake Gaillard Water Treatment Plant, No. Branford, CT. This plant treats an impounded surface water source. The process includes alum coagulation, flocculation, and anthracite/sand filtration. Table 1 gives UV absorbance and TOC values for each of the samples.
Table 1. TOC and UV Absorbance of samples used for bench scale experiments.
|
Date Sample Collected |
UV Abs., 254 nm (cm-1) |
TOC (mg/L) |
|
7/1/97 |
0.030 |
1.91 |
|
11/14/97 |
0.028 |
2.11 |
|
7/21/98 |
0.029 |
1.97 |
A series of bottle tests was conducted with each sample. For these tests, four-liter batches were prepared by adjusting pH and temperature to the desired values (and diluting with deionized water in some cases). Batches were then chlorinated and dispensed into 300 mL bottles. Table 2 shows the conditions used for the bench scale experiments.
Table 2. Bench scale bottle test experiments.
|
Date Sample Collected |
Set |
N1 |
Cl2 Dose (mg/L) |
Temp. (° C.) |
pH |
[NOM]2 |
|
7/1/97 |
2 |
10 |
4.0 |
15 |
7.3 |
1 |
|
3 |
10 |
1.3 |
15 |
7.3 |
1 |
|
|
4 |
10 |
2.5 |
15 |
6.3 |
1 |
|
|
5 |
10 |
2.5 |
15 |
7.3 |
1 |
|
|
6 |
10 |
2.5 |
15 |
8.5 |
1 |
|
|
7 |
10 |
2.5 |
20 |
7.3 |
1 |
|
|
8 |
10 |
2.5 |
10 |
7.3 |
1 |
|
|
9 |
10 |
2.5 |
2 |
7.3 |
1 |
|
|
10 |
10 |
2.5 |
15 |
7.3 |
0.67 |
|
|
11/14/97 |
1 |
10 |
2.7 |
15 |
7.3 |
1 |
|
2 |
10 |
1.3 |
15 |
7.3 |
1 |
|
|
3 |
10 |
2.7 |
15 |
7.3 |
0.5 |
|
|
4 |
10 |
2.7 |
25 |
7.3 |
1 |
|
|
5 |
10 |
2.7 |
2 |
7.3 |
1 |
|
|
6 |
10 |
2.7 |
15 |
6.3 |
1 |
|
|
7 |
10 |
2.7 |
15 |
8.5 |
1 |
|
|
7/21/98 |
1 |
10 |
2.5 |
15 |
7.3 |
1 |
|
4 |
6 |
2.5 |
2 |
9.0 |
1 |
|
|
5 |
6 |
2.5 |
20 |
9.0 |
1 |
|
|
6 |
6 |
2.5 |
2 |
6.0 |
1 |
|
|
7 |
6 |
2.5 |
20 |
6.0 |
1 |
1
number of individual observations2
fraction of undiluted concentration (varied by dilution with deionized water)Bottles were stored headspace-free in the dark at the desired temperature and removed at intervals for measurement of free chlorine, THMs, and HAAs. Chlorine measurements were made using the DPD Titrimetric Method (25). Trihalomethanes and haloacetic acids were measured using methods similar to EPA Methods 551.1 and 552.2, respectively. Each "set" corresponds to a 4 L batch chlorinated under a specific set of conditions, with 7 to 10 measurements (N) made at intervals ranging from 1 minute to 7 days.
Model Description
Three classes of reactive functional groups within the NOM are hypothesized. These are: 1) Sites that react with chlorine instantly relative to the time scale of interest (minutes to days). These reactions are treated as constants (e.g. "instantaneous chlorine demand") in the model. 2) Sites that react with chlorine (HOCl or OCl-) where the first (rate-limiting) step is second-order (first-order in NOM and first-order in chlorine). These are called S1 sites. 3) S2 sites, where there is a rate-limiting initial step that is first-order in NOM, leading to an active form (S2-) that participates in a faster second-order reaction with HOCl. The prototype for the S2 reaction pathway is the classical haloform reaction of ketones with halogens, where the rate-limiting step (first-order in ketone) is a proton dissociation to form enolate. For the S1 and S2 pathways, a series of faster chlorine-consuming steps follow, producing halogenated and oxidized organic compounds, CO2, and Cl-. The amount of formation of each byproduct is an initial amount (representing "instantaneous" formation) plus the sum of specified fractions of the total site consumption through the S1 and S2 pathways. The rate of chlorine consumption is equal to the total rate of site consumption through each pathway multiplied by stoichiometric coefficients representing consumption in intermediate fast steps. The conceptual reaction mechanism is depicted in schematic form in Figure 1.
Equation (1.1) represents the S1 pathway reaction rate, and equations (1.2), (1.3), and (1.4) represent rates related to the S2 pathway.
(1.1)
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
(1.4)
The terms R1, R21f, R21r and R22 are rates, k'1, k'21f, k'21r, and k'22 are apparent rate constants, and [S1], [S2H], and [S2-] represent NOM site concentrations.
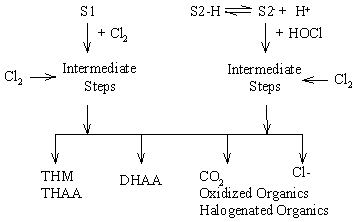
Figure 1. Conceptual Reaction Mechanism
Equations (2) represent the rates of consumption of the reactants (chlorine and NOM sites),
![]()
(2.1)
![]()
(2.2)
![]()
(2.3)
![]()
(2.4)
where n1 and n2 are stoichiometric coefficients that account for chlorine consumption in intermediate steps and the other terms are as described above for equations (1). We have found that the formation kinetics of di- and tri- halogenated HAA species are quite different, so we have treated them as separate groups, with "DHAA" representing the sum of di-halogenated HAA species, and "THAA" representing the sum of tri-halogenated HAA species (Our experiments were conducted using a low-bromide water, so that DHAA= DCAA+BCAA, and THAA=TCAA). We denote total trihalomethane as "TTHM." Equations (3) describe the rates of formation of TTHM, THAA, and DHAA.
![]()
(3.1)
![]()
(3.2)
![]()
(3.3)
The a factors represent the fraction of site consumption through each pathway that results in formation of the respective products.
Equations (1), (2) and (3) comprise the basic framework of the model. The equation system must be integrated using numerical methods. For a particular water and set of environmental conditions, a set of apparent rate constants k', factors n and a, and initial site concentrations [S1], [S2H], and [S2-] can be determined by fitting to experimental data. However, for a particular water, the apparent rate constants and factors may vary with environmental conditions. An important objective is to capture these effects in the model. To achieve this objective, we incorporated a mechanistic treatment of the effects of temperature and pH. Equation (4.1) relates the apparent rate constant k´1 to fundamental rate constants, including temperature and pH effects. Here, k11 and k12 are the rate constants for the reaction of S1 sites with HOCl and OCl- respectively, and aHOCl and aOCl- are pH-dependent distribution factors for the chlorine species. The term q1 with reaction temperature T and reference temperature Tref is the standard engineering representation of the Arrhenius expression.
![]()
(4.1)
Equations (4.2), (4.3), and (4.4) describe the apparent rate constants k´21f, k´21r, and k´22. The rates R21f and R21r represent the forward and reverse components of an acid-base equilibrium reaction, with the forward rate treated as an uncatalyzed reaction with water and the reverse rate dependent on proton concentration.
![]() (4.2)
(4.2)
![]()
(4.3)
![]()
(4.4)
Equations (5) and (6) describe the distribution factors that relate the relative proportions of products to temperature and pH. Our experimental work suggests that substantial THM and THAA formation occurs through competitive pathways. We hypothesize a common pathway leading to a penultimate intermediate that may form either THM by hydrolysis, or THAA by oxidation (21). In our model, the following distribution factors account for the effects of temperature and pH on this hydrolysis/oxidation competition (equations 5):
![]()
(5.1)
![]()
(5.2)
where kp represents uncatalyzed hydrolysis, kP,OH represents base-catalyzed hydrolysis, kP,HOCl represents oxidation, a1,P is the fraction following the hydrolysis pathway, and a2,P is the fraction that follows the oxidation pathway. The distribution factors for the individual byproduct species are linear combinations of the factors given in equations (5). The general form of the distribution factors for individual species is given in equations (6), where the generic subscript DBP denotes TTHM, DHAA, or THAA.
![]()
(6.1)
![]()
(6.2)
In practice, not all of the right hand side terms are included for an individual species: b1 and b2 are included in the DHAA terms, b1, b11, and b21 are included in the THAA terms, and b12, and b22 are included in the TTHM terms.
Calibration and Computation
As stated above, the form of the proposed model is a set of differential equations with known initial conditions that must be solved numerically. Calibration and computational issues are discussed in this section. Two software packages were used for computations and data analysis in this work: the Scientist® data fitting package (26) and a program written by the authors.
Calibration. In order for numerical optimization routines to converge on a solution with the proposed model, initial parameter estimates that are very close to their optimum values are required. We utilized Windows-based computer graphics to make initial parameter estimates. A program was developed that allows adjustment of the model parameters with slide bars while displaying experimental data with the model predictions superimposed. These initial estimates were utilized with the Scientist® (26) software package to find values that resulted in minimum sums of squared residuals. For purposes of model fitting, all response variables were normalized with respect to their average values in the calibration data set. The parameters were optimized with respect to all response variables simultaneously with no weighting. Model parameters and estimated values are presented in Table 3.
Table 3. Model Parameters.
|
Parameter |
Units |
Fitted Value |
|
S1 Path |
||
|
k11 |
m M-1 hr-1 |
0.0347 |
|
k12 |
m M-1 hr-1 |
9.70 x 10-4 |
|
q 1T-20° C |
T in ° C |
1.0996 |
|
S2 Path |
||
|
k21f 1 |
hr-1 |
7.18 x 10-3 |
|
k21r |
m M-1 hr-1 |
1.44 x 107 |
|
k22 |
m M-1 hr-1 |
0.854 |
|
q 21 |
q T-20: T in ° C |
1.089 |
|
Cl2 Demand |
||
|
n12 |
Dimensionless |
8 |
|
n22 |
Dimensionless |
4 |
|
Byproduct Formation |
||
|
kP2 |
Dimensionless |
1 |
|
kP,HOCl |
m M-1 |
0.0620 |
|
kP,OH |
M-1 |
9.82x106 |
|
q P |
q T-20: T in ° C |
1.007 |
|
b 12,THM |
Dimensionless |
0.201 |
|
b 22,THM |
Dimensionless |
0.0956 |
|
b 1,TCAA |
Dimensionless |
0.0387 |
|
b 11,TCAA |
Dimensionless |
0.0272 |
|
b 21,TCAA |
Dimensionless |
0.0777 |
|
b 1,DCAA |
Dimensionless |
0.0346 |
|
b 2,DCAA |
Dimensionless |
0.0345 |
1
Rate assumed to be diffusion-limited. Not treated as adjustable parameter, approximate value from reference (27)2
Fixed arbitrarily, not treated as adjustable parameter.There are two types of parameters in the model: rate constants, and parameters that represent initial NOM site concentrations that cannot be measured and therefore must be determined by fitting the model to experimental data. There are a total of 19 parameters listed in Table 5. Of these, 15 are adjustable, with values estimated by fitting to bench scale data. Rate R21r is assumed to be diffusion limited, and constant k21r is therefore estimated based on a literature value (27). The intermediate step chlorine consumption coefficients n1 and n2 cannot be determined independently from the other rate constants and have been set arbitrarily. The values for n1 and n2 are rough estimates of the chlorine consumed in forming chloroform from dihydroxybenzene and methyl ketone respectively. The byproduct formation parameter kP is not independent of the paramters kPOH and kPHOCL and is therefore set arbitrarily to unity.
Numerical schemes. The Scientist® package includes several numerical routines including an explicit (Euler) scheme, a fourth-order Runge-Kutta scheme, and a scheme designed for stiff equations called the EPISODE scheme (26). We found that the EPISODE scheme produced the best combination of accuracy and computational speed. The scheme used in the in-house program is a second-order mid-point scheme with a time step of 0.1 hours. Under this scheme, explicit response variable estimates at the time-step mid points are used to advance the solution.
Model Comparison
Calibration data set comparison. The proposed model was compared with two other model forms: the power function form described by Amy et al. (6), and the second order form presented by Clark (10, 11). This comparison was intended to evaluate the capacity of the model form to capture the effects of changes in pH, temperature, initial chlorine concentration, and NOM concentration for a specific water. This comparison does not reflect the generality of the models. Each model was calibrated using our bench scale data set. The power function model was calibrated by multiple linear regression using log-transformed variables. The proposed mechanistic model and the second-order model were calibrated using a numerical least-squares minimization routine (26). Results of the comparison are presented in Table 4. Table 4 shows that the mechanistic model gives a superior fit to the data set compared to either the power function or second-order forms, as measured by the adjusted coefficient of multiple determination R2adj, although all three models fit the data well.
Table 4. Comparison of models: calibration data set.
|
Model Form |
|||
|
Parameter |
Mechanistic |
Power Function |
Second-Order |
|
Number of adjustable parameters |
21 |
28 |
25 |
|
Number of data points |
770 |
770 |
770 |
|
Sum of squared observations |
973 |
973 |
973 |
|
Sum of squared deviations |
14.3 |
21.9 |
28.6 |
|
R2adj |
0.985 |
0.971 |
0.970 |
Outside Data Set Comparison. The model was fit to a data set from a different water source, filter effluent from the Robert E. McQaude Water Treatment Plant in Andover, MA (28). This plant treats a blend of pond water and Merrimack River water. The process includes ozonation, alum coagulation, flocculation, settling, and GAC/sand filtration. These data were developed from bench scale experiments similar to the experiments used to develop the calibration data set. Details pertaining to the Andover data set are presented in Table 5. Only the parameters describing initial NOM site, chlorine, THM, and HAA concentrations were adjusted to fit the model to the Andover data set. The values of the parameters listed in Table 3 were not changed. Goodness of fit parameters for the Andover data set are presented in Table 6. Table 7 shows TOC and UV absorbance values for waters used in this work with corresponding model parameters.
Conclusions
A model based on a simplified conceptual reaction mechanism that predicts chlorine decay and the formation of THMs and HAAs was developed and calibrated. The form of the model is a system of differential equations (solved numerically), including fifteen adjustable parameters. Two of these parameters represent reactive site concentrations within the NOM molecules, and are site specific. The other parameters are rate constants and distribution factors that are expected to be more general. In this work, limited testing of the model was performed where the rate constant parameters were calibrated and the model applied to waters from a different source (of similar quality to the calibration source) with good results. We have found the proposed model particularly useful for distribution system modeling where the model was initially calibrated using water from the same source, and only the two NOM site parameters are adjusted to reflect changes in NOM concentration and quality over time.
Table 5. Robert E. McQuade WTP: Bench scale bottle test experiments.
|
Date Sample Collected |
Set |
N1 |
Cl2 Dose (mg/L) |
Temp. (° C.) |
pH |
[NOM]2 |
|
6/97 |
0 |
10 |
2.5 |
20 |
9 |
1 |
|
1 |
7 |
1.25 |
20 |
9 |
1 |
|
|
2 |
9 |
2 |
20 |
9 |
1 |
|
|
3 |
9 |
3 |
20 |
9 |
1 |
|
|
4 |
9 |
2.5 |
8 |
9 |
1 |
|
|
5 |
9 |
2.5 |
15 |
9 |
1 |
|
|
6 |
9 |
2.5 |
20 |
8 |
1 |
|
|
6 |
9 |
2.5 |
20 |
8 |
1 |
|
|
8 |
9 |
2.5 |
20 |
8.5 |
1 |
|
|
9 |
9 |
2.5 |
20 |
9 |
0.5 |
|
|
7/97 |
0 |
9 |
2.5 |
20 |
9 |
1 |
|
1 |
9 |
2 |
20 |
9 |
1 |
|
|
2 |
9 |
2.5 |
20 |
8 |
1 |
|
|
3 |
9 |
2.5 |
9 |
9 |
1 |
|
|
4 |
7 |
2.5 |
20 |
9 |
0.5 |
1
number of individual observations2
fraction of undiluted concentration (varied by dilution with deionized water)Future Work. The calibration and test data sets were both developed using low-bromide waters, and the proposed model does not include bromide effects. The presence of bromide is expected to have a substantial affect on both the speciation and total formation of THMs and HAAs. Use of the model with waters containing substantial bromide concentrations might therefore require further refinements.
As stated above, "instantaneous" (in the time scale of minutes to days) byproduct formation and chlorine demand are treated as constants in the proposed model. Representation of instantaneous formation as a constant is based on the assumption that the total instantaneous demand and formation from fast-reacting NOM sites remains constant for different environmental conditions, although the kinetics may be different. This assumption may not be valid for all waters, and it should be noted that instantaneous chlorine demand and byproduct formation may represent a substantial fraction of the total. A more detailed representation of fast reactions in the model might therefore be required in some cases.
Table 6. Andover data set fit.
|
Parameter |
Value |
|
Number of data points |
491 |
|
Sum of squared observations |
613 |
|
Sum of squared deviations |
38.5 |
|
R2adj |
0.934 |
Table 7. NOM characteristics, "instantaneous" byproduct formation, and initial site concentrations.
|
Water Source |
NOM Characteristics |
Initial NOM site concentrations |
"Instantaneous" byproduct formation |
|||||
|
TOC (mg/L) |
UV 254 (cm-1) |
S1o (mM) |
S2o (mM) |
THMo (mM) |
DCAAo (mM) |
TCAAo (mM) |
||
|
Calibration Set A1 |
1.91 |
0.030 |
1.027 |
8.00 |
0.054 |
0.071 |
0.051 |
|
|
Calibration Set B1 |
2.11 |
0.027 |
1.14 |
6.32 |
0.070 |
0.040 |
0.017 |
|
|
Calibration Set C1 |
2.08 |
0.028 |
1.27 |
7.25 |
0.054 |
0.074 |
0.047 |
|
|
Andover Set 12 |
1.73 |
0.033 |
0.617 |
1.79 |
0.040 |
0.031 |
2.2e-3 |
|
|
Andover Set 22 |
1.73 |
0.033 |
0.335 |
2.24 |
0.035 |
0.036 |
5.9e-3 |
|
1
Lake Gaillard Water Treatment Plant, North Branford, CT-South Central CT Regional Water Authority2
Robert E. McQuade Water Treatment Plant, Andover, MA-Town of Andover3
Typical value-measured value for sample not available
Acknowledgements
The funding for this research provided by the South Central Connecticut Regional Water Authority is gratefully acknowledged. The authors would also like to thank John Affinito, Tom Whitbread and Jeff Johnson at the Lake Gaillard Water Treatment Plant and John Pollano at the Robert E. McQuade Water Treatment Plant for their cooperation in providing water samples used in this work.
Acronyms
BCAA bromochloroacetic acid
DCAA dichloroacetic acid
DBP disinfection byproduct
DHAA sum of di-halogenated HAA species
HAA haloacetic acid
NOM natural organic matter
TCAA trichloroacetic acid
THAA sum of tri-halogenated HAA species
THM trihalomethane
TOC total organic carbon
TTHM total trihalomethane (sum of four species)
USEPA United States Environmental Protection Agency
UV ultra-violet
List of Symbols
|
a 1,THM a 2,THM a 1,TCAA a 2,TCAA a 1,DCAA a 2,DCAA |
factors relating byproduct formation and NOM site consumption |
|
a HOCl, aOCl- |
pH-dependent distribution factors for the chlorine species |
|
a 1P, a 2P |
distribution factors accounting for pH and oxidant concentration effects on byproduct speciation |
|
b 12,THM, b22,THM, b1,TCAA, b11,TCAA, b21,TCAA, b1,DCAA, b2,DCAA |
factors representing the fractional contributions of NOM site classes, and uncatalyzed, oxidation, and hydrolysis pathways to the formation of individual byproduct species |
|
q 1, q 2f, q P |
rate adjusting coefficients for temperature effects |
|
[Cl2] |
free chlorine concentration |
|
[HOCl], [OCl-] |
hypochlorous acid, hypochlorite concentrations |
|
[S1], [S2H], [S2-] |
NOM site concentrations |
|
k1, k21f, k21r, k22 |
rate constants |
|
k¢ 1, k¢ 21f, k¢ 21r, and k¢ 22 |
apparent rate constants |
|
kP, kP,OH, kP,HOCl |
coefficients representing the relative importance of uncatalyzed, hydrolysis, and oxidation pathways in byproduct formation |
|
n1, n2 |
factors relating chlorine demand and NOM site consumption |
|
R1, R21f, R21r R22 |
reaction rates |
|
T, Tref |
Temperatures |
|
R2adj |
adjusted coefficient of multiple determination |
References
(1) Taras, Michael J. (1950), "Preliminary Studies on the Chlorine Demand of Specific Chemical Compounds," J. AWWA 42:5:462
(2) Feben, Douglas; Taras, Michael J. (1951), "Studies on Chlorine Demand Constants," J. AWWA 43:11:922
(3) Engerholm, Bruce A.; Amy, Gary L. (1983), "A Predictive Model for Chloroform Formation from Humic Acid," J. AWWA 75:8:418
(4) Urano, K.; Wada, H.; Takemasa, T. (1983), "Empirical Rate Equation for Trihalomethane Formation with Chlorination of Humic Substances in Water," Water Research 17:12:1797
(5) Edzwald, James K. (1986), "Conventional Water Treatment and Direct Filtration: Treatment and Removal of TOC and Trihalomethane Precursors," in Organic Carcinogens in Drinking Water N. Ram, E. J. Calabrese, and R. F. Christman, eds., John Wiley and Sons
(6) Amy, Gary L.; Chadik, Paul A.; Chowdhury, Zaid K. (1987), "Developing Models for Predicting Trihalomethane Formation Potential and Kinetics," J. AWWA 79:7:89
(7) Montgomery Watson (1993), Final Report: Mathematical Modeling of the Formation of THMs and HAAs in Chlorinated Natural Waters, American Water Works Association, Denver
(8) MacNeill, Andrew L. (1994), Mechanistic Modeling of Trihalomethanes and other Neutral Chlorination By-Products Master's Project, Dept. of Civil and Environmental Engineering, University of Massachusetts at Amherst
(9) Jadas-Hécart, A.; El Morer, A.; Stitou, M.; Bouillot, P.; Legube, B. (1992), "Modelisation De La Demande En Chlore D'une Eau Traitee," Water Res. 26:8:1073
(10) Clark, Robert M. (1998), "Chorine Demand and TTHM Formation: A Second-Order Model," Journal of Environmental Engineering, ASCE 124:1:16
(11) Clark, Robert M. (1998), "Predicting Chlorine Residuals and Formation of TTHMs in Drinking Water," Journal of Environmental Engineering, ASCE 124:12:1203
(12) Vasconcelos, John J.; Grayman, Walter M.; Kiene, Laurent; Wable, Oliver; Biswas. Pratim; Bhari, Ajay; Rossman, Lewis A.; Clark, Robert M., Goodrich, James A. (1996), Characterization and Modeling of Chlorine Decay in Distribution Systems, AWWA Research Foundation, Denver CO
(13) Bell, R. P.; Gelles, E.; Moller, Eva (1949), "Kinetics of the base-catalyzed halogenation of some ketones and esters," Proceedings of the Royal Society of London 198:308
(14) Bell, R. P.; Gelles, E. (1952a), "Equilibria in the halogenation of some organic substances in aqueous solution," Proceedings of the Royal Society of London 210:310
(15) Bell, R. P.; Fluendy, M. A. D. (1963), "Intramolecular Catalysis in the Halogenation of Keto-acids," Transactions of the Faraday Society 59:1623
(16) Rook, Johannes J. (1977), "Chlorination Reactions of Fulvic Acids in Natural Waters," Environmental Science and Technology 11:5:479
(17) Christman, Russell F.; Johnson, J. D.; Haas, J. R.; Pfaender, F. K.; Liao, W. T.; Norwood, D. L.; Alexander, H. J. (1978), "Natural and Model Aquatic Humics: Reactions with Chlorine," Water Chlorination: Environmental Impacts and Health Effects Volume 2, Robert L. Jolley et al., eds., Ann Arbor Science Publishers, Inc., Ann Arbor, MI
(18) Norwood, Daniel L.; Johnson, J. Donald; Christman, Russell F.; Haas, J. Ronald; Bobenrieth, Marie J. (1980), "Reactions of Chlorine with Selected Aromatic Models of Aqueous Humic Material," Envrionmental Science and Technology 14:2:187
(19) Boyce, Scott D.; Hornig, James F. (1983), "Reaction Pathways of Trihalomethane Formation from the Halogenation of Dihydroxyaromatic Model Compounds for Humic Acid," Environmental Science and Technology 17:4:202
(20) Larson, Richard A.; Rockwell, Arelene L. (1979), "Chloroform and Clorophenol Production by Decarboxylation of Natural Acids during Aqueous Chlorination," Envrionmental Science and Technology 13:3:325
(21) Reckhow, David A.; Singer, Phillip C. (1985), "Mechanisms of Organic Halide Formation During Fulvic Acid Chlorinations and Implications with Respect to Preozonation," Water Chlorination: Environmental Impacts and Health Effects Volume 5, Robert L. Jolley et al., eds., Ann Arbor Science Publishers, Inc., Ann Arbor, MI
(22) Rebenne, Laurence M., Gonzalez, Alicia C., Olson, Terese M. (1996), "Aqueous Chlorination Kinetics of Substituted Dihydroxybenzenes," Environmental Science and Technology 30:7:2235
(23) Morris, J. Carrell (1985), "Reaction Dynamics in Water Chlorination," Water Chlorination: Environmental Impacts and Health Effects Volume 5, Robert L. Jolley et al., eds., Ann Arbor Science Publishers, Inc., Ann Arbor, MI
(24) Gurol, Mirat T.; Wowk, Areta; Myers, Samuel; Suffet, Irwin H. (1983), "Kinetics and Mechanism of Haloform Formation: Chloroform Formation from Trichloroacetone," Water Chlorination: Environmental Impacts and Health Effects Volume 4, Robert L. Jolley et al., eds., Ann Arbor Science Publishers, Inc., Ann Arbor, MI
(25) APHA (1992), Standard Methods for the Examination of Water and Wastewater 18th Edition, APHA, AWWA, WPCF, Washington D.C.
(26) MicroMath, Inc. (1995), Scientist® for Experimental Data Fitting/ Microsoft Windows® Version 2.0, software package and user’s manual, MicroMath, Inc., Salt Lake City
(27) Brezonik, Patrick L. (1994), Chemical Kinetics and Process Dynamics in Aquatic Systems, Lewis Publishers, Ann Arbor, MI
(28) Bjorn, Andrew (1997), unpublished data, Department of Civil and Environmental Engineering, University of Massachusetts at Amherst