|
CEE 680 |
|
15 November 2007 |
SECOND EXAM
Closed book, two pages of notes allowed.
Answer all questions. Please state any additional assumptions you made, and show all work.
1. Carbonate System.
(50% for both parts) Two raw drinking waters are mixed as they enter the headworks of a water treatment plant. The two are characterized as follows:
|
Water |
Flow (MGD) |
Alkalinity (mg/L as CaCO3) |
pH |
|
#1 |
20 |
5 |
6.50 |
|
#2 |
10 |
350 |
8.85 |
A. What will the pH of the blended water be immediately after mixing?
B. What will the pH of the blended water be after it has reached equilibrium with the bulk atmosphere?
Solution to Problem #1
Part A.
This is a closed system problem. Therefore the total carbonate concentrations (CT's) must be determined and treated as conservative. Likewise the alkalinities are conservative, and then the final pH can be determined from the blended CT and alkalinity.
for either water:
![]()
first, I would determine the alpha's at the two pH's. Recall the general equations for a diprotic acid are:
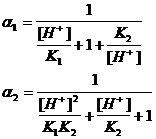
This results in the following values (assuming pKs of 6.3 and 10.3:
|
pH |
alpha-1 |
alpha-2 |
|
6.50 |
0.6130 |
0.0000972 |
|
8.85 |
0.9631 |
0.03417 |
so, for water #1:
CT = {(5/50,000) - (10-7.50) + (10-6.50)}/(0.6130 + 2*0.0000972) = 0.000164 M
and for water #2:
CT = {(350/50,000) - (10-5.15) + (10-8.85)}/(0.9631 + 2*0.03417) = 0.00678 M
now we need to calculate the blended alkalinities and total carbonates:
Alk = (2*5 + 350)/3/50,000 = 0.00240 equ/L
CT = (2*0.000164 + 0.00678)/3 = 0.002369 M
Now calculate the pH from the earlier equation for total carbonates, and making any one of the following three sets of simplifying assumptions:
1.
Alk
is large compared to [OH] and [H]
![]()
which becomes:
![]()
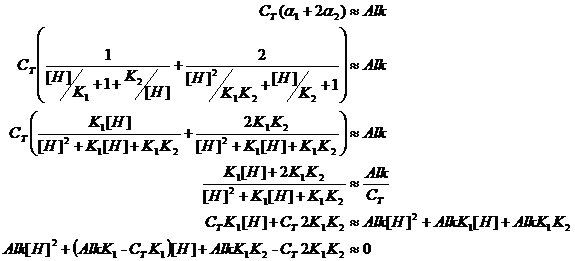
Now use the quadratic equation:
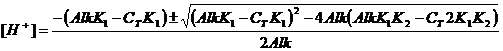
which is simplified to:
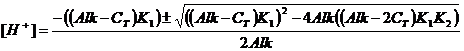
and (Alk – CT) is 0.00240–0.002369 = -0.000031
and (Alk – 2CT) is 0.00240–2(0.002369) = –0.0023378
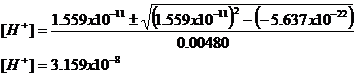
or
pH = 8.574
2.
pH
>> pK1 and Alk is large compared to [OH] and [H]
![]()
which becomes:
![]()
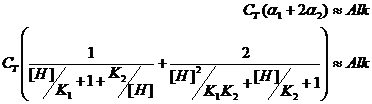
But if pH>>pK1, then we can ignore the first terms in the denominator of each of the two alpha quotients. So this equation simplifies to:
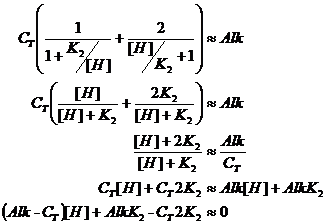
Now we can solve directly for H+:
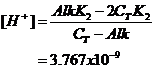
or
pH = 8.424
3.
HCO3->>
CO3-2, pH >> pK1 and Alk is large
compared to [OH] and [H]
![]()
which becomes:
![]()
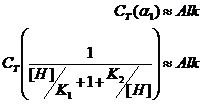
But if pH>>pK1, then we can ignore the first terms in the denominator of the alpha quotient. So this equation simplifies to:
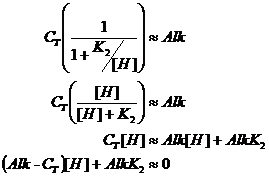
Now we can solve directly for H+:
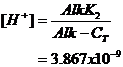
or
pH = 8.413
or,
4.
Make
no assumptions and solve for the exact solution. This gives:
pH = 8.546
Part B.
This is now an open system problem.
There are many ways to solve this, depending on the extent of simplifying assumptions you’re willing to try. Here are a few examples:
1.
Assume
that H+ and OH- are insignificant
![]()
Since this is an open system, we know what CT is:
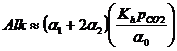
And now:
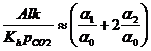
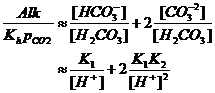
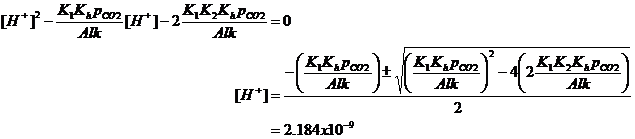
or
pH = 8.66
2.
Assume
that bicarbonate is the only carbonate species of any importance.
Charge balance considerations dictate that:
Alk = CT
Under conditions where pK1 << pH<< pK2, the following is approximately true:
CT = [HCO3-]
And from the equilibrium equation we can conclude:
[HCO3-] = K1 [H2CO3*]/[H+]
And since this is an open system, we can say:
[H2CO3*] = KH pCO2
which becomes, for the bulk atmosphere at 25oC
[H2CO3*] = 10-5
we can combine and get the equation for alkalinity (or bicarbonate) vs H+ in an open system
Alk = [HCO3-] = K1 10-5 /[H+]
Then substituting and isolating H+, we get
[H+] = 10-11.3/Alk
and substituting in for the blended water alkalinity
[H+] = 10-11.3/0.00240
[H+] = 2.088 x 10-9
or
pH = 8.68
2. Complexation
(40%
for both parts) Aqueous
bromide forms strong complexes with many metals. The following two part problem concerns
complexes with silver.
A.
(20%)
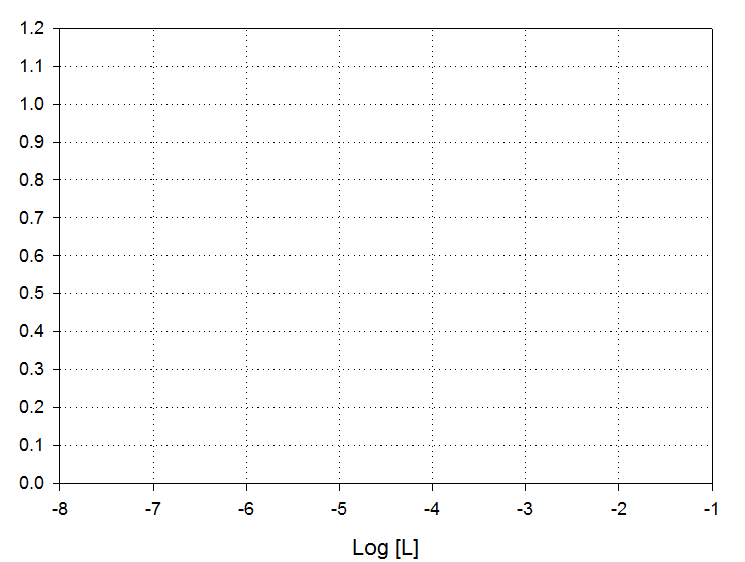
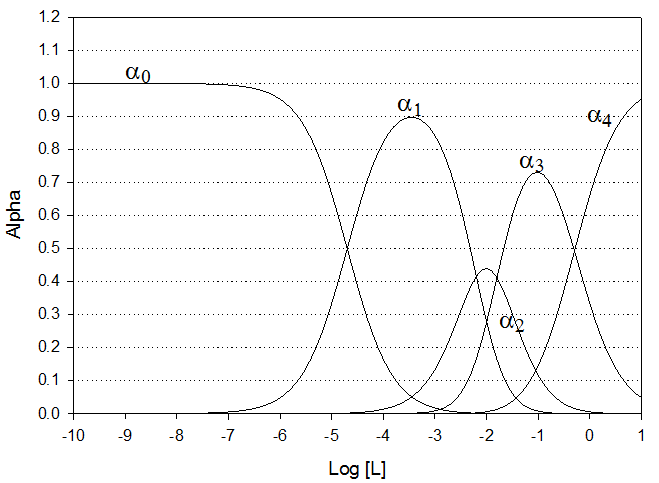
Attached is an accurate graph of alpha values (vs log[ Br-]) for the
Silver-bromide system (equilibria data shown below). Using this graph determine the
complete species composition when the total silver concentration is 20 mM and
the total bromide concentration is 10 mM.
Ignore the possible formation of any
other complexes other than those from Ag and Br; also ignore any possible
precipitation reactions.
B.
(20%)
Describe in qualitative terms the impacts of addition of a very powerful ligand
such as EDTA to this mixture. Estimate
in quantitative terms what the concentrations of each of the species would be
if the total EDTA added was 10 mM, and explain how you got these.
Solution to Problem #2
Part A
The two n-bar curves intersect at a Log[L] of about -4.7. At this point the various alpha values can be read off the graph. They are
Values from the graph as read at Log[L] = -4.7
|
Curve |
α-value |
Species |
Conc (M) |
|
α0 |
0.50 |
Ag+ |
0.010 |
|
α1 |
0.50 |
AgBr |
0.010 |
|
α2 |
0 |
AgBr2- |
0 |
|
α3 |
0 |
AgBr3-2 |
0 |
|
α4 |
0 |
AgBr4-3 |
0 |
Part B.
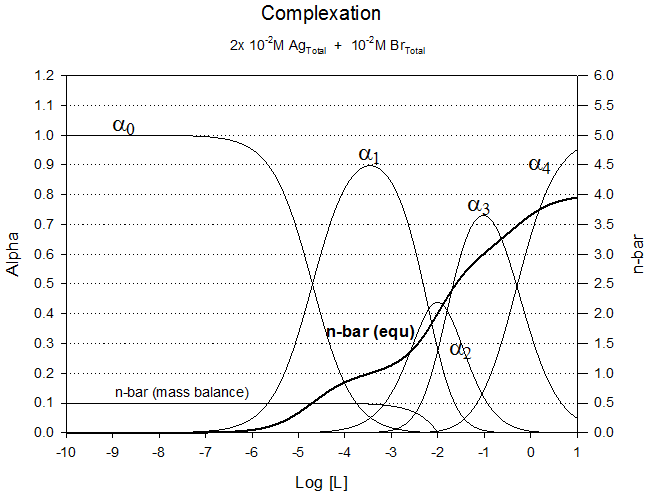
Recognize that the EDTA will completely complex the Silver to until the EDTA is exhausted. This will tie up 10 mM of silver, leaving 10 mM free to complex with the weaker ligand, bromide. This essentially changes the problem to one where the total silver is only 10 mM, so a new n-bar curve based on mass balance can be drawn.
The two n-bar curves intersect at a Log[L] of about -3.5. At this point the various alpha values can be read off the graph. Now the 10 mM of silver not complexed by EDTA is almost entirely (about 90%) in the form of a single AgBr complex, with about 5% free Ag+ and 5% as AgBr2-.
Values from the graph as read at Log[L] = -3.5
|
Curve |
α-value |
Species |
Conc (M) |
|
α0 |
0.05 |
Ag+ |
0.0005 |
|
α1 |
0.90 |
AgBr |
0.0090 |
|
α2 |
0.05 |
AgBr2- |
0.0005 |
|
α3 |
0 |
AgBr3-2 |
0 |
|
α4 |
0 |
AgBr4-3 |
0 |
3. Multiple Choice.
(10%) Answer all 10 of the following questions. Indicate which of the options is the best choice.
1. Benjamin is:
a. the last name of your textbook’s author
b. the first name of your textbook’s author
c. the first name of the current US president
d. a unit of hardness
e. one of the halogens
2. When a solution spontaneously absorbs CO2 from the atmosphere it:
a. results in higher total carbonate
b. drops in pH
c. approaches equilibrium
d. all of the above
e. none of the above
3. Phosphate
a. is a hexadentate ligand
b. is a deadly poison
c. is insoluble
d. is the drug of choice for malaria
e. has been used as a “builder” in detergents
4. H2CO3*:
a. is composed mostly of aqueous CO2
b. is always conservative, even in open systems
c. is a republican
d. all of the above
e. complexes very strongly with sodium
5. Ion pairs:
a. are always charged
b. are larger than
c. are illegal in Montana
d. are outer-sphere complexes
6. The coordination number:
a. is usually 6 or less
b. is related to the charge on the central atom
c. is a function of the size of the ligand
d. all of the above
e. none of the obove
7. The buffer intensity of the open carbonate system:[1]
a. is independent of the alkalinity
b. is
c. is always higher than the pCO2
d. is at a minimum where H+=HCO3-
e. is at a minimum where the pH = pK2
8. Detergent “builders” are used to:
a. help solubilize grease
b. complex trace metals
c. take hardness cations from the surfactants
d. elevate the acidity
e. reduce the caloric content
9. EDTA
a. stands for ethylene dinitro tetraacetic acid
b. is most commonly used as a pH buffer
c. is a higly potent carcinogen
d. is never used because no-one knows what it stands for
e. is a multi-dentate ligand
10. The
a. is a means of estimating alkalinity
b. describes the inverse proportionality of acidity to alkalinity
c. includes a number of books, such as The Chapman Report, and The Prize
d. provides a comprehensive description of ligand structure
e. follows the increase in ligand affinity from Mn(II) to Cu(II)
Selected Acidity Constants (Aqueous Solution, 25°C, I = 0)
|
NAME |
FORMULA |
pKa |
|
|
Perchloric acid |
HClO4 = H+ + ClO4- |
-7 STRONG |
|
|
Hydrochloric acid |
HCl = H+ + Cl- |
-3 |
|
|
Sulfuric acid |
H2SO4= H+ + HSO4- |
-3 (&2) ACIDS |
|
|
Nitric acid |
HNO3 = H+ + NO3- |
-0 |
|
|
Hydronium ion |
H3O+ = H+ + H2O |
0 |
|
|
Trichloroacetic acid |
CCl3COOH = H+ + CCl3COO- |
0.70 |
|
|
Iodic acid |
HIO3 = H+ + IO3- |
0.8 |
|
|
Bisulfate ion |
HSO4- = H+ +
SO4-2 |
2 |
|
|
Phosphoric acid |
H3PO4 = H+ + H2PO4- |
2.15 (&7.2,12.3) |
|
|
Citric acid |
C3H5O(COOH)3=
H+ + C3H5O(COOH)2COO- |
3.14 (&4.77,6.4) |
|
|
Hydrofluoric acid |
HF = H+
+ F- |
3.2 |
|
|
m-Hydroxybenzoic acid |
C6H4(OH)COOH = H+ + C6H4(OH)COO- |
4.06 (&9.92) |
|
|
p-Hydroxybenzoic acid |
C6H4(OH)COOH = H+ + C6H4(OH)COO- |
4.48 (&9.32) |
|
|
Nitrous acid |
HNO2 = H+ + NO2- |
4.5 |
|
|
Acetic acid |
CH3COOH = H+ + CH3COO- |
4.75 |
|
|
Propionic acid |
C2H5COOH = H+ + C2H5COO- |
4.87 |
|
|
Carbonic acid |
H2CO3 = H+ + HCO3- |
6.35 (&10.33) |
|
|
Hydrogen sulfide |
H2S = H+ + HS- |
7.02 (&13.9) |
|
|
Dihydrogen phosphate |
H2PO4- = H+
+ HPO4-2 |
7.2 |
|
|
Hypochlorous acid |
HOCl = H+
+ OCl- |
7.5 |
|
|
Boric acid |
B(OH)3 + H2O = H+ + B(OH)4- |
9.2 (&12.7,13.8) |
|
|
Ammonium ion |
NH4+ = H+ + NH3 |
9.24 |
|
|
Hydrocyanic acid |
HCN = H+
+ CN- |
9.3 |
|
|
p-Hydroxybenzoic acid |
C6H4(OH)COO- = H+ + C6H4(O)COO-2 |
9.32 |
|
|
Phenol |
C6H5OH = H+ + C6H5O- |
9.9 |
|
|
m-Hydroxybenzoic acid |
C6H4(OH)COO- = H+ + C6H4(O)COO-2 |
9.92 |
|
|
Bicarbonate ion |
HCO3- = H+ + CO3-2 |
10.33 |
|
|
Monohydrogen phosphate |
HPO4-2 = H+ + PO4-3 |
12.3 |
|
|
Bisulfide ion |
HS- = H+ + S-2 |
13.9 |
|
|
Water |
H2O = H+ + |
14.00 |
|
|
Methane |
CH4 = H+ + CH3- |
34 |
|