|
CEE 670 |
Fall 2010 |
Kinetics Homework #2
1.
1 Point
The data
below are for the decomposition of Dichloroacetonitrile (DCAN) at pH 7, and 20
C. One column is for and ionic strength
of 0.01 M (mostly NaCl), and the other for 0.03 M. Analyze these data and make any conclusions
you can regarding the nature of the hydrolysis reaction of DCAN.
|
|
DCAN
Concentration (µg/L) |
|
|
Time
(hours) |
I
= 0.01 M |
I
= 0.03 M |
|
0.00 |
44.49 |
44.74 |
|
0.75 |
41.10 |
42.29 |
|
1.50 |
43.73 |
41.64 |
|
2.50 |
38.84 |
37.87 |
|
3.50 |
38.27 |
38.45 |
|
6.50 |
29.22 |
31.97 |
|
9.50 |
26.94 |
29.17 |
|
19.50 |
16.25 |
19.31 |
|
24.50 |
12.66 |
16.44 |
|
29.50 |
9.52 |
13.49 |
|
41.50 |
5.42 |
10.06 |
|
69.50 |
1.55 |
3.83 |
|
116.50 |
|
2.05 |
Solution
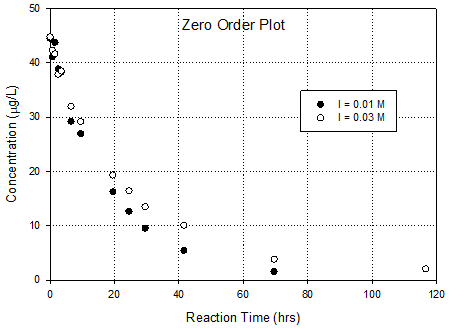
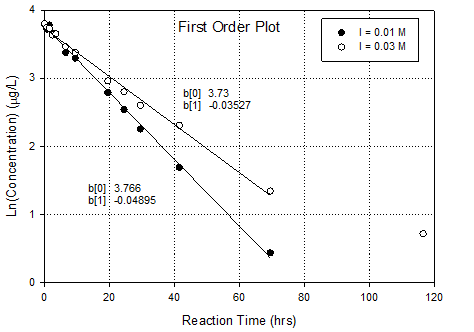
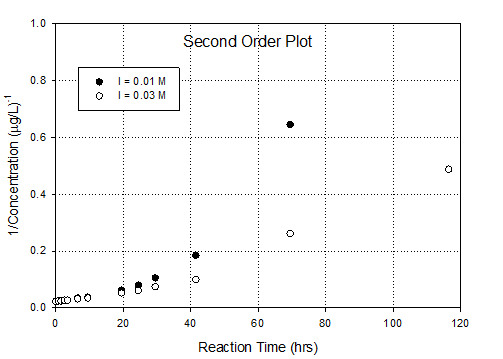
This is an ideal data set for use of the integral
method of kinetic analysis. So, I’d prepare
0 order, 1st order and 2nd order graphs based on integral
method. Then you can assess the relative
fit of the kinetic order. It also allows
you to calculate rate constants.
·
Conclusion is that 1st
order in DCAN fits best, especially when last point in the high ionic
strength dataset is ignored. Why ignore
that data point? Because log transform
accentuates its importance in a linear regression (expands the error). One presumes that error is essentially
constant in the un-transformed data
·
Rate constant goes
up as ionic strength goes down; 0.035hr-1 to 0.049hr-1.
·
Direction and magnitude of ionic strength effects implies
that reaction is between a negative
species (hydroxide) and a species with a positive center (maybe the
carbon on the nitrile).
2.
1 Point
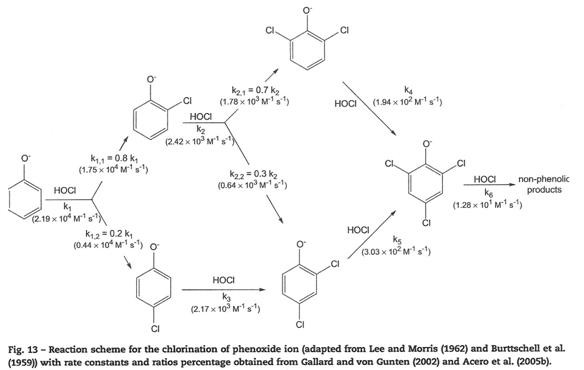
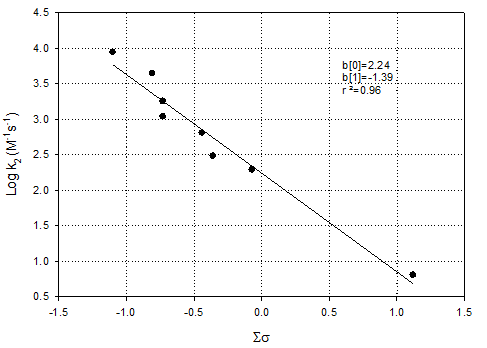
Prepare
a Hammett Plot for the chlorination of phenol at high pH (i.e., phenate
ions). Use all of the rate constants in
Figure 13 from Deborde & von Gunten, 2008 [Water Research 42:13-51]. To
help you with this you should number each carbon and treat the attack on
different carbon atoms separately even if they result in the same product. Use the Hammett substituent constants in the
attached table. Compare your results
with those obtained by Deborde & von Gunten in their Figure 15.
Solution:
I used benzene as the implicit “reference compound” instead of
phenate, because attack on phenate can occur at the ortho, meta or para
positions (3 different scenarios, and effectively 3 different reference
reactions). In contrast, attack on
benzene is only on one carbon as they are all identical.
This requires that you include the phenoxy (-O-) group
explicitly in your Hammett Plots.
Also, I included the last reaction (k6), presuming attack
on both open ring positions (identical).
Many chose not to include this reaction, presumably because the exact
products are not known. This is fine,
but it give different answers as noted below.