Many types of reactions can be expressed as an equilibrium between the reactants and products. With acid/base reactions, and complexation reactions this equilibrium is reached very quickly. However, adsorption, precipitation, and redox reactions tend to approach equlilibrium much more slowly. In many of these cases one cannot assume that the systems are at equlibrium, so that the kinetics of approach to equilibrium must be considered. However, thermodynamics is generally better understood, and more predictable than kinetics. For this reason, the use of thermodynamic equilibria is often the first and most reliable means of attacking a chemical problem.

The derivation of thermodynamic equilibria used here is based on the kinetic arguments presented in Chapter IV. Consider a general reaction between two species, AB and CD (equation 5.1). In order to form the products, the two reactants must first come into physical contact with each other. Once this happens there is a certain, finite probability (based on their kinetic energy and relative geometric positions) that reaction 5.1 will take place. As with nearly all chemical equations, the reverse reaction may also occur (reversible reactions). This would involve the physical approach of species AC and BD, followed by some reaction (with a different probability of occurrance).

AB + CD « AC + BD (5.1)

The rate (v) of either the forward or reverse reaction may be expressed as the product of the frequency of intermolecular contact (Fc) and the probability of reaction given that intermolecular contact has occurred (Pr).

v = PrFc (5.2)

The frequency of intermolecular contact will be equal to the probability of intermolecular contact (Pc) for any two specific molecules times the number of these molecules present. It will also depend on the diffusivity of the species (a function of temperature).

Combining equations 5.2 and 5.3 we get:

Factoring in the volume of solution and Avogadro's number, one gets and equation in terms of concentration of the reactants and a single lumped probablility term that is called the reaction rate constant, k.

v = k [reactant#1] [reactant#2] (5.5)

Now applying this to the reaction in equation 5.1, we can write two rates, one for the forward reaction, and one for the reverse.

vf = kf [AB] [CD] (5.6)

vr = kr [AC] [BD] (5.7)

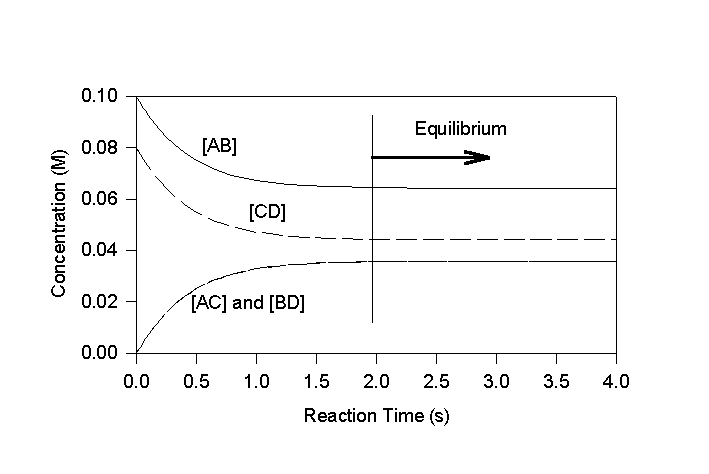
When a pure solution of AB is added to a pure solution of CD, the forward reaction proceeds initially at a much faster rate than the reverse. This continues until a significant amount of the products, AC and BD accumulate (Figure 5.1). Eventually equilibrium is reached when the rate of the forward reaction exactly equals the rate of the reverse reaction. The concentration of the four species at equilibrium is then fixed by the relative reaction rates (equation 5.6 & 5.7).

Figure 5.1

Concentration Profiles for Reaction Between Two Hypothetical Species

(kf=10 M-1s-1 and kr=22 M-1s-1)

at equilibrium:

vf = vr (5.8)

and:

kf [AB] [CD] = kr [AC] [BD] (5.9)

The equilibrium constant is defined as the ratio of the forward to reverse reaction rate constants.