Consider a reaction in the gas phase between molecules of hydrogen and iodine.

H2 + I2 -----> 2 HI (4.1)

The rate at which this reaction occurs will depend on a number of factors such as the concentration of hydrogen and iodine in the reacting gas. In order for a molecule of hydrogen and a molecule of iodine to combine to form hydrogen iodide, the two molecules must come into contact with each other (contact meaning approach within a certain distance so that bonding forces can play a role).

Imagine a chamber containing 100 molecules of hydrogen and only 1 molecule of iodine. Eventually the molecule of iodine will, by random motion, contact a hydrogen molecule in such a way as to form hydrogen iodide. This may take some time, however, due to the small number of hydrogen molecules available for contact. If the number of hydrogens is doubled, one would expect the formation of hydrogen iodide to occur twice as fast. On the other hand, if the number of iodine molecules was increased to 10, the rate at which any one of the iodine molecules forms hydrogen iodide would be unchanged, but the overall rate of hydrogen iodide formation would increase by a factor of 10. Thus, a general rate law for hydrogen iodide formation can be written, based on the simple concept of probability of molecular contact. That is, the rate of formation of the reaction product is proportional to the number of molecules of one reactant times the number of molecules of the second reactant. This is the kinetic law of mass action. This principle is the same whether we're dealing with numbers of molecules or molar concentrations of molecules. Equation 4.2 is the common form for this reaction rate law.

(4.2)

where the reactants and products are expressed in molar concentrations and kf is called the forward reaction rate constant. The units for kf are liters/mole per unit time. The reaction tate is going to be a function of such things as the rate of movement of the molecules, and the probability of HI formation given that a collision between hydrogen and iodine has already occurred.

Most of the simple reactions discussed here occur in a single phase. These are termed Homogeneous Reactions and they usually involve dissolved species. Many environmentally important reactions involve species in different phases, and these are termed Heterogeneous Reactions. An example of a heterogeneous reaction is the dissolution of calcitic minerals in acidic waters. Such reactions involve both a transfer step and a reaction step. If the transfer step is slow, they are said to be transport-limited. If the chemical reaction step is slow, they are reaction-limited.

Consider a homogeneous reaction of the following type:

aA + bB ------> cC + dD (4.3)

where the capital letters represent chemical species participating in the reaction and the small letters are the stoichiometric coefficients (i.e., the numbers of each molecule or ion required for the reaction). In most cases the rate law will be of the form:

(4.4)

Note that, depending on your frame of reference, equation 4.4 could also be writted as:

(4.5)

where:

(4.6)

The overall order of reaction 4.3 is (a+b). The order with respect to species A is a, and the order with respect to species B is b.

Homogeneous reactions may be either elementary or non-elementary. Elementary reactions are those reactions that occur exactly as they are written, without any intermediate steps. These reactions almost always involve just one or two reactants. The number of molecules or ions involved in elementary reactions is called the molecularity of the reaction. Thus, for all elementary reactions, the overall order equals the molecularity. Non-elementary reactions involve a series of two or more elementary reactions. Many complex environmental reactions are non-elementary. In general, reactions with an overall reaction order greater than two, or reactions with some non-integer reaction order are non-elementary.

Reaction rate constants can be evaluated from experimental data by any one of four techniques: the integral method; the excess method; the differential method; and the initial rate method.

This method allows one to use most or all of the experimental data in determining rate constants. However, one must first be certain of the reaction stoichiometry before attempting this kinetic analysis. In the following paragraphs, a series of linearizations are presented depending on the reaction order. If the exact reaction order is uncertain, one may try several different linearizations. The best fit should occur with the linearization that is appropriate for the data (i.e., indicating the correct reaction order).

For zero order reactions, the rate is simply a constant.

(4.7)

Integrating equation 4.7 gives:

(4.8)

Thus, the reaction rate constant is obtained from the slope of a plot of the molar concentration of "C" (i.e., [Ct]) versus reaction time. The intercept is, of course, the initial concentration ([C]o).

For first order reactions, the rate is proportional to one of the reactants to the 1st power.

(4.9)

Integrating equation 4.9 gives:

(4.10)

Thus, the experimental data are plotted with natural log of the concentration on the y-axis and time on the x-axis. The reaction rate constant is simply the negative of the slope of this line, and the intercept is the natural log of the initial concentration.

For second order reactions, the rate is proportional to one of the reactants to the 2nd power, or to two reactants, each to the 1st power. For the former case the following rate equation holds.

(4.11)

Integrating equation 4.11 gives:

(4.12)

Thus, the experimental data are plotted as the reciprocal concentration (y-axis) versus time (x-axis). The reaction rate constant is simply the slope of this line, and the intercept is the reciprocal of the initial concentration.

Some second and higher order reactions are more easily examined when one reactant is essentially held constant. This can be done by using a large excess of one of the reactants such that fractional change in concentration over the course of reaction is negligible. For example, if reaction 4.3 is allowed to proceed with "B" originally present at a concentration 50 times greater than "A", then the rate expression reduces to:

(4.13)

where "k" can be treated as a constant with respect to time:

(4.14)

The rate law expressed by equation 4.13 is said to be pseudo-ath order. This means that although the reaction is fundamentally of order (a+b), it appears to be of order "a" in the experiments. Kinetic analysis of 4.13 is much easier than 4.4. This also relieves the need to measure "B" throughout the experiment (i.e., it is unchanging).

Some complicated kinetic systems cannot be analyzed by the integral method, with or without the use of an excess. In these cases either the differential, or the initial rate methods should be employed. The differential method has the advantage of allowing one to use all of the experimental data.

The simplest case would be for a reaction which is some non-integer order with respect to a reactant. If the reaction is dependent on another reactant, the excess method can be employed to suppress this effect. Experimental data for the reactant are plotted as a function of reaction time. A smooth curve is drawn through these data, and tangents are drawn to the curve at various points. The slope of each one of these tangents gives the instantaneous reaction rate. These rates are then plotted versus concentration of the species being followed on a log-log scale. The slope of the line formed gives the reaction order with respect to this constituent.

Use of the initial rate method requires that many separate experiments be run. However, for reactions of changing order and dependency, this is the best method of analysis. As with the differential method, a smooth curve is drawn through the concentration vs time data. Here, only a tangent to the curve at the origin is constructed. The slope gives the initial rate of this reaction, the rate at time=0, when the solution composition is well known. Experiments with different starting concentrations are run and a single initial rate is determined for each. This is a very versatile method, and it is not subject to competitive or catalytic pathways initiated by reaction products.

As mentioned previously, the reaction rate constant, k, is a function of temperature. The Arrhenius equation (4.15) is the classic model.

(4.15)

where ko is the called the frequency factor, or the pre-exponential factor, Ea is the activation energy, R is the universal gas constant (199 cal/°K-mole), and T is the temperature in °K. The natural log of the reaction rates are plotted as a function of the reciprocal absolute temperature. The slope is then -Ea/R and the intercept is lnko. In environmental engineering, equation 4.16 is often used to describe the relationship between temperature and reaction rate constants.

(4.16)

where k20 is the value of the rate constant at 20°C, T is the temperature in °C, and R is an empirically derived constant, usually between 1.0 and 1.2. Although, equation 4.16 is not based in chemical theory, as 4.15 is; it is more covenient to use. Over short spans of temperature equation 4.16 gives results that are similar to 4.15.

Dissolved oxygen will readily oxidize ferrous iron (+II) to ferric (+III) hydroxide according to the following stoichiometry:

O2 + 4Fe(+II) + 8OH- + 2H2O -------------> 4Fe(OH)3 (4.17)

The observed reaction rate law is:

(4.18)

where k = 2.8±1.3 x1015 liter3/Mole3/min at 20.5°C (Stumm & Lee, 1961).

The reaction is catalyzed by certain metals (e.g., Cu+2, Co+2) and anions capable of complexing ferric iron (e.g., phosphates, H3SiO4-). This means that in the presence of such chemical substances, the reaction actually proceeds faster than indicated by equation 4.18.

The formation of trihalomethanes may occur through many different reaction mechanisms. One of the most widely discussed is the haloform reaction (Figure 4.1). This involves the stepwise chlorine substitution of the enolate form of a methyl ketone. The resulting trichloroacetyl compound undergoes base hydrolysis liberating chloroform and a carboxylic acid.

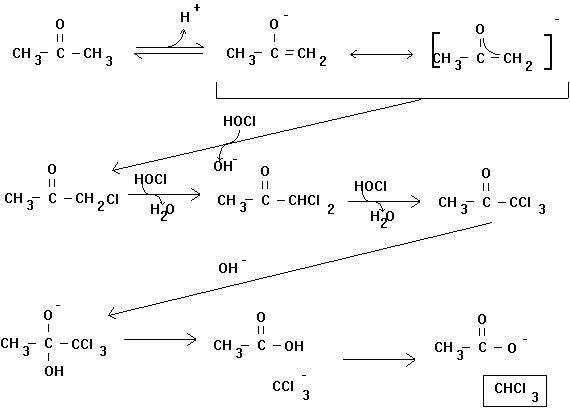
Figure 4.1

The Haloform Reaction

Many early studies with acetone (propanone) indicated that the rate limiting step was the initial enolization. Once the enolate was formed, the molecule proceeded through the entire reaction pathway. Thus, the reaction rate expression often cited in the chemical literature was:

(4.19)

However, under environmental conditions (i.e., neutral pH, low chlorine residual) other steps may be rate limiting. This changes the rate law, and complicates attempts to characterize it. In fact, this is not even the complete mechanism for the chlorination of acetone. Trichloropropanone may undergo further base-catalyzed chlorine substitution to form pentachloropropanone (see Figure 4.2). This compound will rapidly hydrolyze to form chloroform and dichloroacetic acid. The rate law proposed for the loss of trichloropropanone is:

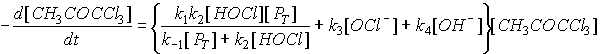(4.20)

Compounds other than the simple methyl ketones may react with chlorine via numerous pathways to form trihalomethanes. These mechanisms may include activated aromatic substitution of chlorine, chlorine addition reactions, oxidation reactions, hydrolysis reactions and rearrangements.

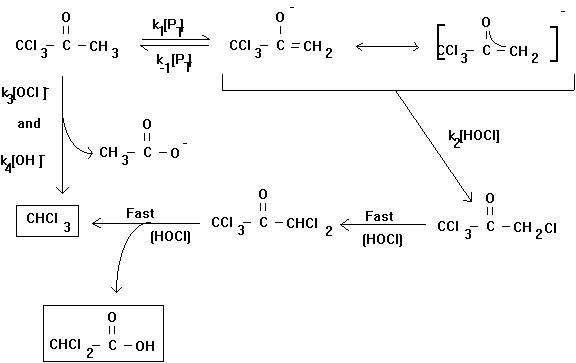
Figure 4.2

Proposed Mechanism for the Chlorination of 1,1,1-Trichloropropanone

(after Reckhow and Singer, 1985)

Chlorine will readily react with trace quantities of bromide to form hypobromous acid.

HOCl + Br- ---------> HOBr + Cl- (4.21)

The speed of this reaction is such that it rapidly proceeds until there is very little bromide left. The hypobromous acid formed can then react with organic matter reforming bromide which completes the cycle.

d[HOBr]/dt = (3.1x103 l/M-sec)[HOCl][Br-] (4.22)

Therefore, in the presence of bromide, the active halogen shifts from chlorine to bromine. This is significant, because bromine may react differently with organic matter than chlorine does. For example, bromine is far more reactive with acetone, forming an order of magnitude more trihalomethane (i.e., bromoform) than with chlorine. On the other hand chlorine gives higher concentrations of trihalomethanes with resorcinol than bromine. With natural waters and aquatic fulvic acids, the presence of bromide usually supports an increase in THM production. Studies with extracted aquatic humic material have shown a a sharp loss of TCAA and DCAA with increasing bromide concentrations (Croué, 1987). It is likely that some bromoacetic acids and brominated THMs are formed in their place.