ELEMENTARY CHEMICAL PRINCIPLES
The periodic table of the elements lists atomic numbers and atomic weights for each element. The atomic numbers, the number of protons in each atom, is not commonly used in environmental analysis. However, the atomic weights are quite useful. They represent the total weight of each atom in atomic mass units (AMU) or Daltons. For many elements the tabulated atomic weights represent an average of the atomic weights of each of the naturally occurring isotopes weighted according to their abundance in the biosphere. Table 2.1 is an alphabetical list of the stable elements with their atomic numbers and weights. A periodic table appears as Figure II-1.
1. Types of bonds
a. Ionic Bonds - transfer of an electron to complete an octet.
atoms to ions
Nao + Clo --------> NaCl or Na+ + Cl- (2.1)
![]() (2.2)
(2.2)
b. Covalent Bonds - sharing of one or more electron pairs
Single bond
2 H + O -----------> H-O-H (2.3)
![]() (2.4)
(2.4)
Double bond
2 O --------------> O=O (2.5)
![]() (2.6)
(2.6)
2. Valence.
An atom's valence is the number of chemical bonds it makes with other atoms, including ionic and covalent. Many elements have more than one valence, as noted in Table 2.1. Elements in the first column in the periodic table (i.e., the alkali metals; sodium, potassium, etc.) all have a valence of 1. They are therefore called monovalent metals. Those in the second column (i.e., the alkaline earths; magnesium, calcium, etc.) have a valence of 2, and are called divalent.
Oxidation State is characterized by an oxidation number which is the charge one would expect for an atom if it were to dissociate from the surrounding molecule or ion. It may be either a positive or negative number, usually, an integer between -VII and +VII (Roman numerals are generally used to represent oxidation number). This concept is useful in balancing chemical equations and performing certain calculations. The rules for calculating oxidation number are as follows:
a. The oxidation number for atoms or ions simply equals the charge of the species. For example the oxidation number of sodium, Na+, or chloride, Cl-, ions is +I and -I respectively.
b. The oxidation number of atoms in an elemental molecule or homonuclear covalent molecule (e.g., oxygen, O=O) is zero.
c. The oxidation number of atoms in a covalent non-elemental molecule is determined in a stepwise fashion. Heteronuclear covalent bonds (i.e., where different atoms are joined together by a covalent bond) are generally polar, that is, the electrons are not shared evenly between the two atoms. Oxidation number is determined by imagining the charge that would exist if these polar bonds were to become completely ionic. In other words, the oxidation number is the charge on each atom after all bonding electrons have been assigned to the more electronegative of the two atoms joined by each bond. In general, the less metallic an atom is (the closer it is to the upper right hand corner of the periodic table), the more electronegative it is. However, when uncertain, one should consult Pauling's comparative electronegativities (see Table 2.1). Where the two atoms are identical, the covalent bond is non-polar and the bonding electrons are split evenly.
In most cases one can assign all hydrogens an oxidation state of +I (exception: hydrides[-I]), and oxygen an oxidation state of -II (exception: peroxides[-I]). Then, the molecule is split at the bonds between similar atoms (e.g., C-C and C=C bonds). The sum of all the valences in each fragment of the molecule must equal the overall charge of that portion of the molecule (usually zero). From this constraint, the oxidation state of the remaining atoms (usually carbon, nitrogen and sulfur) can be determined.
Table 2.1
Properties of the Stable Elements
|
Element |
Symbol |
Atomic # |
Atomic Wt. |
Valence |
Electronegativity |
|
Aluminum |
Al |
13 |
26.98 |
3 |
1.47 |
|
Antimony |
Sb |
51 |
121.75 |
3,5 |
1.82 |
|
Argon |
Ar |
18 |
39.95 |
0 |
|
|
Arsenic |
As |
33 |
74.92 |
3,5 |
2.20 |
|
Barium |
Ba |
56 |
137.34 |
2 |
0.97 |
|
Beryllium |
Be |
4 |
9.01 |
2 |
1.47 |
|
Bismuth |
Bi |
83 |
208.98 |
3,5 |
1.67 |
|
Boron |
B |
5 |
10.81 |
3 |
2.01 |
|
Bromine |
Br |
35 |
79.91 |
1,3,5,7 |
2.74 |
|
Cadmium |
Cd |
48 |
112.40 |
2 |
1.46 |
|
Calcium |
Ca |
20 |
40.08 |
2 |
1.04 |
|
Carbon |
C |
6 |
12.01 |
2,4 |
2.50 |
|
Cerium |
Ce |
58 |
140.12 |
3,4 |
1.06 |
|
Cesium |
Cs |
55 |
132.91 |
1 |
0.86 |
|
Chlorine |
Cl |
17 |
35.45 |
1,3,5,7 |
2.83 |
|
Chromium |
Cr |
24 |
52.00 |
2,3,6 |
1.56 |
|
Cobalt |
Co |
27 |
58.93 |
2,3 |
1.70 |
|
Copper |
Cu |
29 |
63.54 |
1,2 |
1.75 |
|
Dysprosium |
Cy |
66 |
162.50 |
3 |
1.10 |
|
Erbium |
Er |
68 |
167.26 |
3 |
1.11 |
|
Europium |
Eu |
63 |
151.96 |
2,3 |
1.01 |
|
Fluorine |
F |
9 |
19.00 |
1 |
4.10 |
|
Gadolinium |
Gd |
64 |
157.25 |
3 |
1.11 |
|
Gallium |
Ga |
31 |
69.72 |
2,3 |
1.82 |
|
Germanium |
Ge |
32 |
72.59 |
4 |
2.02 |
|
Gold |
Au |
79 |
196.97 |
1,3 |
1.42 |
|
Hafnium |
Hf |
72 |
178.49 |
4 |
1.23 |
|
Helium |
He |
2 |
4.00 |
0 |
|
|
Holmiuum |
Ho |
67 |
164.93 |
3 |
1.10 |
|
Hydrogen |
H |
1 |
1.01 |
1 |
2.20 |
|
Indium |
In |
49 |
114.82 |
3 |
1.49 |
|
Iodine |
I |
53 |
126.90 |
1,3,5,7 |
2.21 |
|
Iron |
Fe |
26 |
55.85 |
2,3 |
1.64 |
|
Krypton |
Kr |
36 |
83.80 |
0 |
|
|
Lanthanium |
La |
57 |
138.91 |
3 |
1.08 |
|
Lead |
Pb |
82 |
207.19 |
2,4 |
1.55 |
|
Lithium |
Li |
3 |
6.94 |
1 |
0.97 |
|
Lutetium |
Lu |
71 |
174.97 |
3 |
1.14 |
|
Magnesium |
Mg |
12 |
24.31 |
2 |
1.23 |
|
Manganese |
Mn |
25 |
54.94 |
2,3,4,6,7 |
1.60 |
Table 2.1 cont.
Properties of the Stable Elements
|
Element |
Symbol |
Atomic # |
Atomic Wt. |
Valence |
Electronegativity |
|
Mercury |
Hg |
80 |
200.59 |
1,2 |
1.44 |
|
Molybdenum |
Mo |
42 |
95.94 |
3,4,6 |
1.30 |
|
Neodymium |
Nd |
60 |
144.24 |
3 |
1.30 |
|
Neon |
Ne |
10 |
20.18 |
0 |
1.07 |
|
Nickel |
Ni |
28 |
58.71 |
2,3 |
1.75 |
|
Niobium |
Nb |
41 |
92.91 |
3,5 |
1.23 |
|
Nitrogen |
N |
7 |
14.01 |
3,5 |
3.07 |
|
Osmium |
Os |
76 |
190.2 |
2,3,4,8 |
1.52 |
|
Oxygen |
O |
8 |
16.00 |
2 |
3.50 |
|
Palladium |
Pd |
46 |
106.4 |
2,4,6 |
1.39 |
|
Phosphorus |
P |
15 |
30.97 |
3,5 |
2.06 |
|
Platinum |
Pt |
78 |
195.09 |
2,4 |
1.44 |
|
Potassium |
K |
19 |
39.10 |
1 |
0.91 |
|
Praseodymium |
Pr |
59 |
140.91 |
3 |
1.07 |
|
Rhenium |
Re |
75 |
186.2 |
1.46 |
|
|
Rhodium |
Rh |
45 |
102.91 |
3 |
1.45 |
|
Rubidium |
Rb |
37 |
85.47 |
1 |
0.89 |
|
Ruthenium |
Ru |
44 |
101.07 |
3,4,6,8 |
1.42 |
|
Samarium |
Sm |
62 |
150.35 |
2,3 |
1.07 |
|
Scandium |
Sc |
21 |
44.96 |
3 |
1.20 |
|
Selenium |
Se |
34 |
78.96 |
2,4,6 |
2.48 |
|
Silicon |
Si |
14 |
28.09 |
4 |
1.74 |
|
Silver |
Ag |
47 |
107.87 |
1 |
1.42 |
|
Sodium |
Na |
11 |
22.99 |
1 |
1.01 |
|
Strontium |
Sr |
38 |
87.62 |
2 |
0.99 |
|
Sulfur |
S |
16 |
32.06 |
2,4,6 |
2.44 |
|
Tantalum |
Ta |
73 |
180.95 |
5 |
1.33 |
|
Tellurium |
Te |
52 |
127.60 |
2,4,6 |
2.01 |
|
Terbium |
Tb |
65 |
158.92 |
3 |
1.10 |
|
Thallium |
Tl |
81 |
204.37 |
1,3 |
1.44 |
|
Thorium |
Th |
90 |
232.04 |
4 |
1.11 |
|
Thulium |
Tm |
69 |
168.93 |
3 |
1.11 |
|
Tin |
Sn |
50 |
118.69 |
2,4 |
1.72 |
|
Titanium |
Ti |
22 |
47.90 |
3,4 |
1.32 |
|
Tungsten |
W |
74 |
183.85 |
6 |
1.40 |
|
Uranium |
U |
92 |
238.03 |
4,6 |
1.22 |
|
Vanadium |
V |
23 |
50.94 |
3,5 |
1.45 |
|
Xenon |
Xe |
54 |
131.30 |
0 |
|
|
Ytterbium |
Y |
39 |
88.91 |
2,3 |
1.06 |
|
Zinc |
Zn |
30 |
65.37 |
2 |
1.66 |
|
Zirconium |
Zr |
40 |
91.22 |
4 |
1.22 |
Table 2.2
Common Inorganic Polyatomic Ions
|
Name |
Formula |
Charge |
Special Nomenclature |
|
Ammonium |
NH4 |
+1 |
|
|
Hyroxide |
OH |
-1 |
|
|
Bicarbonate |
HCO3 |
-1 |
H2CO3-carbonic acid |
|
Cyanide |
CN |
-1 |
|
|
Nitrate |
NO3 |
-1 |
HNO3-nitric acid |
|
Nitrite |
NO2 |
-1 |
HNO2-nitrous acid |
|
Permanganate |
MnO4 |
-1 |
|
|
Hypochlorite |
OCl |
-1 |
HOCl-hypochlorous acid |
|
Iodate |
IO3 |
-1 |
|
|
Chlorate |
ClO3 |
-1 |
|
|
Bromate |
BrO3 |
-1 |
|
|
Chlorite |
ClO2 |
-1 |
|
|
Chlorate |
ClO3 |
-1 |
|
|
Perchlorate |
ClO4 |
-1 |
HClO4-perchloric acid |
|
Metaphosphate |
PO3 |
-1 |
HPO3-metaphosphoric acid |
|
Carbonate |
CO3 |
-2 |
|
|
Sulfate |
SO4 |
-2 |
H2SO4-sulfuric acid |
|
Sulfite |
SO3 |
-2 |
H2SO3-sulfurous acid |
|
Thiosulfate |
S2O3 |
-2 |
|
|
Chromate |
CrO4 |
-2 |
|
|
Dichromate |
Cr2O7 |
-2 |
|
|
Phosphate (ortho-phosphate) |
PO4 |
-3 |
H3PO4-phosphoric acid |
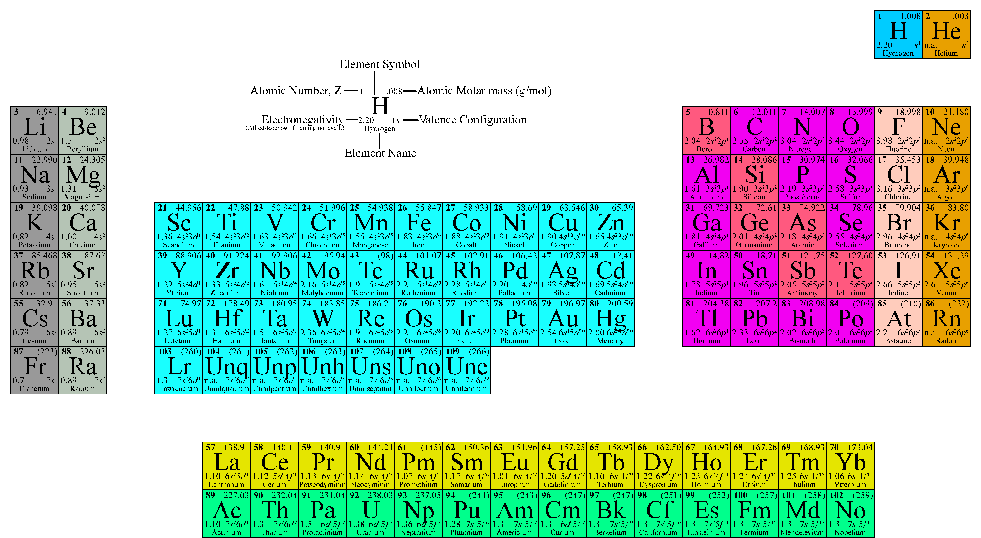
Figure -1 Periodic Table of the Elements
Example 2.1: What is the oxidation state of the atoms in acetic acid?
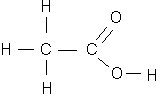
First we know that hydrogen probably has an oxidation state of +I, and oxygen is -II. Then, we can break the atom at the carbon-carbon bond, and each half must have a total oxidation state of zero. Therefore, the carbon on the left-hand side must have an oxidation state of -III, and the one on the right side, +III. This is an example of the variable oxidation state of carbon, which ranges from -4 for methane, to +4 for carbon dioxide. Carbon may even be present in different oxidation states in the same molecule, as illustrated by this example.
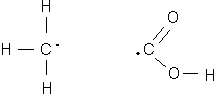
Quantitative analytical chemistry is based on the ability to measure concentration and express it in an unambiguous way. In the environmental sciences, concentrations can be expressed on a mass basis, a molar basis, or an equivalent basis.
1. Mass Basis. This is simply an expression of the mass of analyte per volume of sample (e.g., per liter for an aqueous sample). Since most waters and wastewaters have a density nearly equal to pure water, one liter of these samples may be explicitly equated to one kilogram. Thus, for example, a 1 mg/L concentration might be expressed as 1 mg/kg. This is a dimensionless number equal to 1/1,000,000 or 1 part per million. For this reason, concentrations of mg/L and ppm are often used interchangeably. Table 2.3 lists mass/volume concentrations commonly used in the environmental field with equivalent mass/mass units for aqueous samples.
Table 2.3
Common Mass-Based Concentration Units
|
Mass/Volume Units |
Mass/Mass Units |
Typical Applications |
|
g/L (grams/liter) |
(parts per thousand) |
Stock solutions |
|
mg/L (milligrams/liter)10-3g/L |
ppm (parts per million) |
Conventional pollutants (DO, nitrate, chloride) |
|
µg/L (micrograms/liter)10-6g/L |
ppb (parts per billion) |
Trihalomethanes, Phenols. |
|
ng/L (nanograms/liter)10-9g/L |
ppt (parts per trillion) |
PCBs, Dioxins |
|
pg/L (picograms/liter)10-12g/L |
Pheromones |
For highly concentrated stock solutions, especially acids and bases, concentrations are sometimes expressed as the ratio of commercial compound to water. For example, 1 + 3 HCl is prepared by adding one volume of hydrochloric acid (conc.) to three parts distilled water. Thus, it is 25% of the concentration of commercial concentrated hydrochloric acid.
Concentration can also refer to a specific part of a molecule. For example, a solution of potassium sulfite will contain a certain concentration of K2SO3. However, one may wish to know the concentration of sulfite only, or perhaps any one of the elemental constituents: potassium, sulfur or oxygen.
2. Molar Concentrations. Molar concentrations are expressed as the number of moles of a substance present in one liter volume. A mole is a gram molecular weight (GMW) or more generally, a gram formula weight (GFW) of a substance. This corresponds to the quantity of substance in grams which is equal to the atomic weight of the substance, whether it be an atom, a molecule or an ion. The utility of these units is that one mole contains the same number of atoms, molecules or ions (Avogadro's Number, 6.02x10
23) regardless of the identity of the substance. A solution of 1 mole of a substance dissolved in a liter of water (i.e, 1 mole/L) is called a 1 Molar solution, and is said to have a Molarity of one. ![]()
![]()
![]()
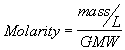 (2.7a)
(2.7a)
or more generally:
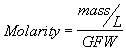
![]() (2.7b)
(2.7b)
Example 2.2: What is the concentration in grams/liter of a 1 Molar solution of ammonium sulfate, (NH4)2SO4?
2 x MW(N) = 2 x 14 = 28
8 x MW(H) = 8 x 1 = 8
1 x MW(S) = 1 x 32 = 32
4 x MW(O) = 4 x 16 = 64
GMW = 132
Answer: 132 g/L.
Sometimes the term Formality is used when reactive substances like acids and bases are concerned. This is a measure of the amount of moles of any pure substance added per liter of solution. With formality, the chemist makes no assumptions about the final form of the diluted substance. For example, consider the addition of 1 Mole of acetic acid to a liter of water. A significant fraction of that acid will donate its proton to water forming acetate and H3O+. While it is common to refer to such a solution as 1 Molar in acetic acid, it is really something less than 1.0 M CH3COOH. Nevertheless, we can avoid such ambiguities by saying that the solution is 1.0 Formal in acetic acid, and it will be understood that some of the acid might exist in the deprotonated form.
3. Equivalent Concentrations. Equivalent concentration or normality is commonly used with acid/base or oxidation/reduction reactions. It is calculated such that one equivalent of a substance will react with exactly one equivalent of another substance. A 1 Normal solution contains 1 gram equivalent weight (GEW) of a substance per liter of volume.
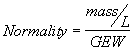 (2.8)
(2.8)
A gram equivalent weight is the mass of the substance which contains one gram atom of "available" hydrogen or its equivalent.
![]() (2.9)
(2.9)
where Z is some positive integer (usually 1,2, or 3) which represents the number of equivalents per mole. A solution containing one equivalent per liter is said to be 1 Normal (or 1 N). Solutions of fractional normality are often expressed as a fraction; for example, 0.25 Normal may be abbreviated as N/4.
From equations 2.7, 2.8 and 2.9, the following relationship between molarity and normality can be derived. Note that since Z is generally equal to or greater than unity, the normality of a solution will be equal to or greater than its molarity.
Normality = Molarity * Z (2.10)
For acids, Z is simply the number of protons that will be donated.
Z = 1, for monoprotic acids (e.g., hydrochloric acid or acetic acid)
HCl ---------> H+ + Cl- (2.11)
CH3COOH -----> CH3COO- + H+ (2.12)
Z = 2, for diprotic acids (e.g., sulfuric acid)
H2SO4 --------> 2H+ + SO4-2 (2.13)
Z = 3, for triprotic acids (e.g., phosphoric acid)
H3PO4 --------> 3H+ + PO4-3 (2.14)
For bases, Z is the number of hydroxide ions liberated, because one hydroxide neutralizes one proton to form water.
Z = 1, for mono-hydroxides (e.g., sodium hydroxide)
NaOH ® Na+ + OH- (2.15)
Z = 2, for di-hydroxides (e.g., calcium hydroxide)
Ca(OH)2 ® Ca+ + 2OH- (2.16)
For species undergoing oxidation or reduction (redox) reactions, Z is the number of electrons transferred per molecule.
Z = 1, for single electron transfers, such as the oxidation of ferrous iron to ferric iron.
Fe+2 ® Fe+3 + e- (2.17)
Z = 6, for six electron transfers, such as the reduction of potassium dichromate to trivalent chromium.
K2Cr2O7 + 7H+ + 6e- ® 2K+ + 2Cr+3 + 7OH- (2.18)
For other reactions such as precipitation or complexation, Z will depend on the particular stoichiometry. However, in most cases the value of Z will be equal to the value of the oxidation state of the atom (or group) that will be reacting times the number of these atoms (or groups) that are bound in the reacting molecule. For example there are two atoms of Al(+III) in one molecule of alum (Al2(SO4)3 18H2O). Therefore, the Z value for alum is equal to six.
Example 2.3: Consider a solution of Ammonium Sulfate prepared by dissolving 66 g of the anhydrous compound in water and diluting to 1 liter. What is the concentration of this solution in:
a) g/L?
b) moles/L?
c) equivalents/L?
d) g/L as sulfate?
e) g/L as N?
Answer:
a) 66 g/L
b) In example 2.1, the gram molecular weight of ammonium sulfate was determined to be 132 g/mole. So, using equation 2.7, on gets:
Molarity = (66 g/L)/(132 g/mole) = 0.5 moles/L or 0.5 M.
c) Without any specific information regarding the use of this solution, one might simply presume that either the sulfate group or the ammonium group will be the reacting species. In either case, Z should be equal to two (product of the oxidation state times the number of groups). Using equation 2.10, one calculates:
Normality = 0.5 moles/L * 2 equivalents/mole
= 1 equivalent/L or 1.0 N or N/1.
d) The GFW for sulfate is:
GFW = 32 + 4*16 = 96.
The molarity of sulfate is:
Molarity = 0.5 moles-(NH4)2SO4/L * 1 mole-SO4/mole-(NH4)2SO4
= 0.5 moles-SO4/L
Then, rearranging equation 2.7b, one gets:
mass/L = Molarity * GFW = 0.5 moles-SO4/L * 96 g-SO4/mole-SO4
= 48 g-SO4/L
e) The GFW for nitrogen is simply 14:
The molarity of nitrogen is:
Molarity = 0.5 moles-(NH4)2SO4/L * 2 moles-N/mole-(NH4)2SO4
= 1 mole-N/L
Again, rearranging equation 2.7b, one gets:
mass/L = Molarity * GFW = 1 mole-N/L * 14 g-N/mole-N
= 14 g-N/L or 14 g NH3-N/L
4. Molal Concentrations. Molal concentrations are determined from the number of moles of a substance added per kilogram of solution. At STP, the molal concentration is equivalent to the molar concentration. Because mass is conservative, molal concentrations do not change as the temparatuer changes. However, a solution prepared at one temperature will not have the same molar concentration at another temperature. For this reason, molal concentrations are sometimes more convenient than the more common molar units.
pC is defined as the negative of the logarithm of the molar concentration of any chemical species, "C" (equation 2.19). This notation is most commonly used in conjunction with the hydrogen ion concentration (i.e, pH). Since hydrogen ions react with so many species found in water, their concentration is critical to understanding the kinetics and thermodynamics of aquatic chemical processes. It is often easiest to base chemical models of such systems on pH, and as a result pH has been referred to as the "master variable" (see Stumm & Morgan, 1996, Chapt.3)
pC = -log[C] (2.19)
Balanced chemical equations conform to the laws of conservation of mass and conservation of charge. The law of conservation of mass dictates that the total number of atoms of each type on one side of the equation must equal the number on the other. Conservation of charge requires that the net charge of all reactants equal the net charge of all the products. In order to obtain a balanced equation one must start with accurate knowledge of the identity of all reactants and all products. Then the laws of conservation of mass and charge may be satisfied by adjusting the coefficients associated with any of the reactants or products. Frequently, this is not enough. One might also have to add a variable number of water molecules (H2O) or its constituents (H+ or OH-) to either side. This is an acceptable practice, because it is very difficult to determine if these species are produced or consumed by a reaction carried out in dilute aqueous solution. However, it is well established that they are common participants in aqueous-phase reactions.
2.1 Calculate the gram molecular weight of: (a) NaNO3, (b) Mg(OH)2, (c) Al2(SO4)3, (d) KMnO4.
2.2 How much potassium dichromate must be added to a liter of water to make a 0.05 molar solution?
2.3 What is the gram equivalent weight of: (a) HClO4, (b) BaSO4?
2.4 Balance the following equations:
a) CaCl2 + Na2CO3 ® CaCO3 + NaCl
b) MnO2 + NaCl + H2SO4 ® MnSO4 + H2O + Cl2 + Na2SO4
c) C6H4(COOH)2 + O2 ® CO2