CHAPTER XVII:
LIGHT-SCATTERING AND MOLECULAR SPECTROPHOTOMETRY
A. Introduction
Light or electromagnetic radiation can be characterized by wave-like behavior. The wavelength, , is the distance between the crest of one wave and the crest of the next one. The frequency, , is the number of complete waves that pass a reference point in a second. These two are related by the velocity of light, c (3 x 1010 cm/sec), in accordance with equation 17.1.
![]() (17.1)
(17.1)
Alternatively, light may also exhibit behavior resembling that of a particle. These particles, called photons, have a unique energy, E, that is dependent on the frequency (equation 17.2) through Planck's Constant, h.
![]() (17.2)
(17.2)
As a result of equations 17.1 and 17.2, the energy of a photon of light is inversely proportional to its wavelength.
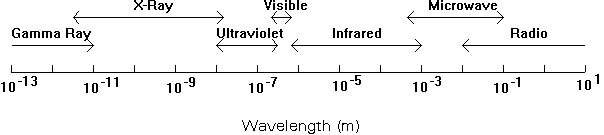
The human eye perceives light of different wavelengths as being comprised of separate colors. When a substance absorbs light of a certain wavelength (color), it depletes the transmitted light in precisely those wavelengths that are absorbed. For this reason, a solution that appears blue to the human eye does not absorb blue light. Rather, it is blue because it absorbed orange light, and allows all other wavelengths to pass unhindered (giving a bluish color to the transmitted light; see Table 17.1).
Table 17.1
Relationship Between Color
and Absorbance
|
Wavelength of absorbance maximum (nm) |
Color Absorbed |
Color Remaining |
|
380-420 |
Violet |
Green-yellow |
|
420-440 |
Violet-blue |
Yellow |
|
440-470 |
Blue |
Orange |
|
470-500 |
Blue-green |
Red |
|
500-520 |
Green |
Purple |
|
520-550 |
Yellow-green |
Violet |
|
550-580 |
Yellow |
Violet-blue |
|
580-620 |
Orange |
Blue |
|
620-680 |
Red |
Blue-green |
|
680-780 |
Purple |
Green |
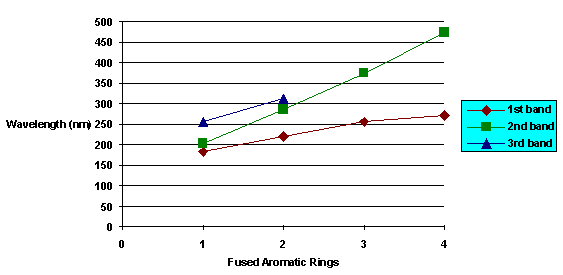
Double bonds are strong absorbers of light, especially when they are arranged in an alternating pattern with carbon-carbon single bonds. This alternating pattern of single bond followed by double bond followed by single bond followed by double bond is called a conjugated double bond system. It has a property known as resonance, which makes it absorb light of high wavelengths (i.e., low energy). The molar absorptivity and wavelength of maximim absorbance generally increases with increasing numbers of conjugated double bonds. This is illustrated by the series of polynuclear aromatic hydrocarbons, below.
When a solution is placed in a path of light, a certain amount of that light will pass through it unaffected. The fraction of the incident light that reaches the other side of a liquid sample will be dependent on the pathlength through the sample, x, and the ability of the sample components to block or otherwise impede the passage of light, , called the extinction coefficient. This relationship is given by Lambert's Law:
![]() (17.3)
(17.3)
or
![]() (17.4)
(17.4)
where:
Io = the intensity or radiant power of the incident light
I = the intensity or radiant power of the light after passing through a though a thickness, x, of the liquid sample
The blockage or impedance of light may be due to scattering or absorption. Light scattering occurs when small particles deflect the light so that it does not reach the other side of the sample. Absorbance is the process by which a constituent (usually dissolved) absorbs the light energy and releases it as heat or stores it as bond energy. Thus, the extinction coefficient in equation 17.3 and 17.4 is composed of two components, the scattering coefficient () and the absorption coefficient ().
![]() (17.5)
(17.5)
B. Light Scattering
When light scattering is large compared to absorption, (i.e., >> ), Lambert's Law reduces to:
![]() (17.6)
(17.6)
The scattering coefficient may be expressed as the product of the concentration of particles, N, and the scattering cross section of those particles, .
![]() (17.7)
(17.7)
The scattering cross section is a measure of the amount of light scattered per particle. It is a function of the size and shape of the particle. For particles of extremely small size (i.e., a diameter 10% of the incident light's wavelength), Rayleigh Scattering predominates. The Rayleigh Scattering cross section for an ideal spherical "particle" is given by equation 17.8.
![]() (17.8)
(17.8)
Thus, the Rayleigh Scattering depends only on the pathlength, the concentration of "particles", the wavelength of the light, , and the polarizability of the light, . Equation 17.8 predicts that the smaller wavelength light will be scattered the most. Therefore, blue light should be scattered more than the other visible wavelengths. As a result, a clear daytime sky appears blue when looking at any direction except directly into the sun.
Larger particles are subject to Mie Scattering. With these large particles, light may scatter all over their surfaces at different angles. Mie Scattering is the type of light scattering that is responsible for turbidity in natural waters. It is far more complex than Rayleigh Scattering, and cannot be described by a simple equation. The Mie Scattering cross section is a function of the particle size and shape as well as the wavelength of light. Maximum cross section for a given wavelength occurs when the particles present are of a size that is similar to the wavelength. Less scattering occurs as the difference between the particle size and wavelength increases.
1. TURBIDITY
a. Environmental Significance
Historically, turbidity is considered a measure of the attenuation of light through a sample of water. However, modern turbidimeters are based on nephelometry, which is the measurement of true light scattering. For this reason, we will use the terms turbidimetry and nephelometry interchangeably to indicate the measurement of light scattering by small particles in a water. These particles may be composed of clays, bacteria, algae, or colloidal organic molecules. Accordingly, the sizes of these particles may range over several orders of magnitude. Turbidity-producing particles are of concern in drinking water supplies for a variety of reasons. Cloudy or turbid waters are aesthetically unpleasing. Thus, consumers may be tempted to forgo an otherwise acceptable disinfected drinking water for one that is not disinfected, but clear. Turbid waters may be less filtrable as a result of the high load of particles applied to the filters. This would obligate shorter filter runs and add to the expense of the finished water. Finally, turbidity-producing particles may serve to protect micro-organisms (e.g., pathogens) and render disinfection processes less effective.
Turbidity measurements are used to assess the quality of water supplies. Knowing raw water turbidities, an engineer can suggest a treatment sequence that is likely to be economically and technologically feasible for any particular source (e.g., conventional treatment vs direct filtration vs in-line filtration; see Weisner et al., 1988). A knowledge of turbidity may also help the engineer to estimate unit sizes and chemical costs (e.g., for coagulation and sludge handling). However, pilot studies must often be performed before a treatment plant is designed; and here again, turbidity measurements are used to assess the effectiveness of most treatments processes one would test. Finally, turbidities are monitored in full-scale treatment installations both for the purpose of process control and for the purpose of establishing compliance with finished water turbidity standards.
b. Measurement: Turbidimetry
Modern methods for determining turbidity employ nephelometric turbidimeters which measure the intensity of light scattered at 90°30° with respect to the incident light. The detector should be sensitive to light in the range of 400-600 nm wavelength. This measurement is then compared to an identical measurement of an accepted turbidity standard. The standards have pre-designated turbidities expressed in nephelometric turbidity units (NTU). Accepted standard substances include formazin, a co-polymer of hydrazine sulfate and hexamethylenetetramine, and commercially-available polystyrene divinylbenzene beads (AEPA-1).
In the UMass Environmental Engineering Teaching Laboratory we have a Hach Model 2100A laboratory turbidimeter. Light from a tungsten filament lamp is projected up through a flat-bottom sample cell. A 90° slit allows scattered light to reach the photomultiplier tube. The photomultiplier is especially sensitive to the ultraviolet light scattered by small particles (i.e., 0.1 to 0.5 microns). The 2100A has a rated bias and precision of -2% of full scale on all ranges. Thus, it is always advisable to use the highest range while still being able to remain on scale. The ranges are 0-0.2, 0-1.0, 0-10, 0-100 and 0-1000 NTU; and the detection limit is 0.04 NTU on the lowest range.
It is not uncommon that the same sample, measured on two different nephelometric instruments may give different turbidity readings. This can occur even though the two instruments may be calibrated against the same standards. Differences in instrument design, bulb age and output voltage may account for this. For example, if the voltage applied to the bulb drops with time, the tungsten filament will become cooler and the output spectrum will shift toward longer wavelengths. Since larger particles are better at scattering light of longer wavelength, this instrument will become more sensitive to larger particles and less sensitive to smaller ones. A formazin standard which has relatively large particles allows one to calibrate the instrument to the larger particles. However, the instrument will no longer be sufficiently responsive to the smaller particles in a water sample. One way of avoiding this problem is calibrate against two different types of standard materials (e.g., formazin and AEPA-1; these have a diameter range of 1.75-20m and 0.2-0.8m, respectively) and adjust the bulb voltage (or replace the bulb, if necessary) until the instument can be calibrated so they both give correct readings. Another source of error is the presence of stray light reaching the photo sensor. Stray light may be determined using a methanol standard.
C. Molecular Spectrophotometry
1. THEORY
When absorption is large compared to light scatter, (i.e., >> ), Lambert's Law reduces to Beer's Law:
![]() (17.9)
(17.9)
The absorption coefficient may be expressed as the product of the concentration of absorbing substances, c, times their molar absorptivity, a.
![]() (17.10)
(17.10)
Therefore, the transmittance (T = I/Io) of a liquid sample is given by equation 17.11.
![]() (17.11)
(17.11)
A more convenient measure of the absorption of a liquid sample is the logarithm of the reciprocal of the transmittance. This value, called the absorbance (A), is linearly related to the concentration of the absorbing substance.
A = -log(T) (17.12)
A = acx (17.13)
Absorbances may also be presented as absorbance units per pathlength, or simply reciprocal pathlength (e.g., as cm 1). We will symbolize this representation of absorbance with Abs.
Abs = A/x = ac (17.14)
Equation 17.14 predicts that a plot of Abs versus concentration will give a straight line with a slope of "a". The absorptivity is commonly expressed in terms of absorbance units per mole/L. This value is called the molar absorptivity.
2. MEASUREMENT
a. Spectrophotometers
Sample absorbances are measured with a spectrophotometer. This is an instrument composed of a light source, a wavelength selector (monochromator), a sample compartment, and a detector. The type of light source will depend on the desired wavelength. Light in the visible range (350nm-800nm) is best supplied by a tungsten filament lamp. Ultraviolet (UV) light (190nm-350nm) requires a deuterium lamp. The wavelength selector splits the light spectrum into its component colors and selects a narrow band of this spectrum. Either a prism or a grating may be used as a dispersing element to split the light. The spectrum is generally projected on an opaque wall containing a slit. The physical width of the slit determines the band width of the selected light. The wavelength of the selected light may be adjusted by changing the angle of the dispersing element, so that the desired wavelength passes through the slit. The selected light passes into the sample compartment, through the sample (and cell) and to the detector (photomultiplier). By measuring transmittance with (I) and without (Io) the sample present, absorbance can be determined. This is how a single beam spectrophotometer operates.
A more accurate and convenient scheme is embodied in the double beam spectrophotometer. This instrument has a chopper motor which alternately deflects the light beam through a reference cell and the sample cell. This is done many times per second, and the average ratio between the two readings gives the transmittance. This is a more accurate method, because it minimizes variabilities due to rapidly changing lamp output or momentary stray light in the detector compartment. In effect, the analyst is continually monitoring and adjusting for changes in the lamp output as measured by the detector.
In the Environmental Engineering teaching laboratory we have several spectrophotometers. One is a Perkin-Elmer Model 111 Ultraviolet-Visible Spectrophotometer. This is a typical single beam instrument with a spectral range of 200-900 nm. It uses a diffraction grating with fixed bandpass of 2.0 nm. The wavelength accuracy is ±0.5 nm and the precision is ±0.1 nm. The photometric linearity is -0.005 absorbance units at a reading of 0.400 absorbance units. The photometric reproducibility is better than 0.01% Transmittance, and stray light is less than 0.5% T at 220 nm. This instrument also has a stability characterized by a drift of less than 0.5% T per 5 min after a 15 min warm-up period. As with most UV-Vis spectrophotometers, the PE 111 uses a Tungsten lamp in the visible region (900-340 nm) and a Deuterium lamp in the ultraviolet region (340-200 nm).
For best operation, spectrophotometers should be installed in air conditioned rooms, free from dust, corrosive fumes, vibrations, and large changes in temperature and humidity. Instructions for calibrating and operating the PE 111 are as follows:
1. With the operation switch in the off position, verify that the meter mechanical zero is correct.
2. Select the proper lamp for the desired wavelength by adjusting the selector lever to either VISIBLE or ULTRAVIOLET.
3. Adjust the wavelength knob to the correct value.
4. Turn on the appropriate lamp. If the deuterium lamp is chosen, the #1 switch must be turned on first, then 20-30 sec later the #2 switch is turned on.
5. Turn the operation switch to "on".
6. Open the cell compartment and insert both filled sample and reference cells in the cell holder. The reference cell belongs in the position #1.
7. Place the operation switch to the "meter" position.
8. With the cell compartment cover open (this automatically closes the shutter), adjust the meter to infinite absorbance (0 transmittance) with the zero adjusting knob.
9. Close the cell compartment cover, and place the reference cell in the light path by adjusting the cell positioning knob. Adjust the meter to 0 absorbance (100% transmittance) with the zero adjusting knob.
10. Pull out the cell positioning knob and read the absorbance of the sample.
Also in the environmental engineering laboratory we have a Spectronic 21 capable of measurement in the UV as well as visible range. This is also a single beam instrument that requires adjustment to 100% transmittance (or zero absorbance) prior to use.

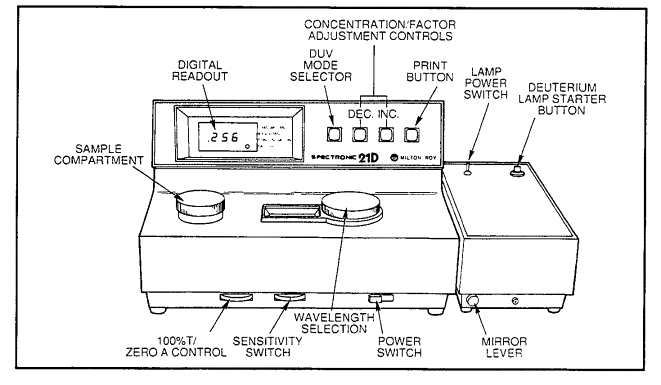
Figure 17.1 Controls on the Spectronic 21D UV-Vis Spectrophotometer
b. Spectrophotometric cells
Cells (or cuvettes) are supplied with varying light paths and different qualities of glass. Most spectrophotometric work is conducted with standard rectangular cells of 1 cm path length. These are square in cross-section and about 4 times as high as they are wide. They generally have a pathlength tolerance of -0.01 mm. In addition, rectangular cells of 0.1, 0.5 and 4 cm are commercially available. For more dilute solutions, cylindrical cells of 5 and 10 cm are available. These have two filler necks into which fit fluoropolymer stoppers. The ability to seal these cells is an attractive feature for volatile or hazardous samples. The cylindrical cells may be supplied with fluoropolymer covers, but these do not make a very good seal. Rectangular cells with extra thick side walls are also available for the analysis of small volumes of liquid. In addition, various types of flow through and jacketed cells are available for kinetic studies, continuous monitoring, and temperature sensitive work.
Cells for absorption spectrophotometry have opposing optically polished windows with frosted glass side walls. Be sure to orient the cells so that the optic windows are perpendicular to the light path. Fluorescence cells are made with all (or adjacent) optically polished windows.
Cells should be cleaned like other laboratory glassware. If detergents prove ineffective, they may be soaked in chromic acid cleaning solution. Note that the windows and side walls are fused forming an acid-proof seal. In addition, quartz cells may also be cleaned by immersing in concentrated nitric acid followed by ultrasonic agitation or 10-15 minutes of boiling in water.
Table 17.2
Spectrophotometric Cells
|
Window |
Wavelength
Range (nm) |
Letter
Code |
Lot
#s |
Color
Code |
|
Optical Glass |
360 - 1000 |
OG |
|
yellow |
|
Near-UV Glass or Special Optical Glass |
300 - 1000 |
OS or SG |
180's |
green |
|
Standard Silica |
220 - 2500 |
|
|
|
|
Supracil Quartz or Quartz UV |
165 - 2600, 2850 - 3600 |
QS or UV |
280's |
blue |
|
Infracil Quartz or Quartz IR |
220 - 3600 |
QI or IR |
300's |
red |
Most spectrophotometric cells sold in the US are marked with a series of letters and numbers. Many are marked with and upper case "SCC" (Scientific Cell Company) and number indicating the path length (e.g., 1.000 for 1 cm) followed by a two letter code, a colored dot or a lot number. These markings will identify the type of glass used in the optical windows (see table below). Cells should always be matched with the same markings including lot number. This is especially important when running absorbance scans. It is of highest importance to choose a cell which is useable for the wavelength chosen. Although any of the cells listed below may be used in the visible range, the optical glass cells are preferred because of their lower cost. For near-UV and UV work, near-UV glass, Supracil quartz or Infracil quartz should be employed depending on the wavelength chosen. In general, the lower the minimum wavelength, the more expensive the cell. For work in the infrared region, Infracil quartz is required.
3. ANALYTICAL MOLECULAR SPECTROPHOTOMETRY
a. Direct Methods
Most specific chemical analytes do not have large enough absorptivity to make their determinations by direct spectrophotometry practical. However, their molar absorptivities may be substantially increased by reaction with color-forming reagents. This is the basis for most colorimetric or spectrophotometric methods. The two exceptions common to environmental engineering are the determination of "color" and "UV absorbing substances". However, color and UV absorbance are somewhat unique in that they are gross parameters which are operationally defined. They are both commonly used to assess the concentration of natural organic matter (e.g., humic substances) in a water. Humic substances absorb strongly over a wide range of wavelengths (see section b). Absorbance measurements will depend on the concentration of the humic substances, the flora and fauna from which the humics were derived, and the solution pH. This last factor is particularly important with respect to the analysis of UV absorbance and color. As pH increases, UV absorbance and particularly, color increase. This is likely due to deprotonation of acidic sites on the humic molecules, causing an unfolding of the molecules and increasing the multiplicity of resonance structures. Regardless of the mechanism, it is important that a water be buffered at a fixed pH (usually 7) prior to analysis for UV absorbance and color.
Color. Natural waters derive color from humic materials and sometimes from metals such as iron and manganese. This is a common means of characterizing a natural water's organic content. Color is very easy to measure, requires only the simplest glassware, and correlates well with DOC or TOC in many water treatment systems. Color is also important because it is a direct measurement of a water's disagreeable visual properties. As a result many treatment systems are designed to remove color whereas the specific goal of removing organic carbon is secondary.
Two types of color are often reported, "true color" and "apparent color". True color is that which is attributed to dissolved species, and it is therefore, the color remaining after a sample is filtered. Apparent color is derived from the absorbance of dissolved species and the light scattering of particles. It is, therefore, measured without prior filtration. The actual determination of color is done by visual comparison or with the aid of a spectrophotometer.
The platinum-cobalt method of visual comparison is the classic procedure used for decades. Color standards are prepared by mixing predetermined amounts of potassium chloroplatinate and cobaltous chloride in water, and diluting this stock 10 to 100 fold. The prescribed ratio of cobalt to platinum gives a yellowish hue characteristic of natural waters. Filtered or unfiltered samples are pH-buffered and placed in 50 mL Nessler tubes. Platinum-cobalt standards are added to similar tubes. Concentrations are in Pt-Co color units. These correspond numerically to the concentration of platinum in mg/L in the standard which most closely resembles the water. Color analysis in the field may be more conveniently conducted with pre-calibrated glass disks.
Color may also be conveniently and precisely measured using a spectrophotometer. The range of wavelengths chosen run from 400 nm to 700 nm, with 400 nm being most common. As before, the samples are buffered at pH 7 and pre-filtered if desired. The color value is simply the absorbance of the sample at the designated wavelength.
UV Absorbance. Most natural organic matter will absorb sufficient ultraviolet (UV) light to be easily detected by a standard UV-Vis spectrophotometer. By convention, we have chosen 254 nm as the wavelength to measure UV absorbance[1]. This parameter is quite important because: (1) it is inexpensive, rapidly measured, and requires a minimum of training; and (2) it has been found to correlate with certain water quality characteristics, such as DOC and THMFP.
UV absorbance has been successfully used as a means of estimating DOC and THM precursor levels in raw waters. However, its most important contribution is to process monitoring. For a single raw water source, coagulation effectiveness can be effectively monitored by UV absorbance. One can generally develop good linear correlations between UV abs and DOC for raw and treated waters from the same plant (e.g., Edzwald et al., 1985). The interpretation changes, however, when a disinfection or oxidation step is encountered. When monitored across oxidation/disinfection, UV absorbance provides information on the degree of oxidation of the natural organic matter in the water.
The specific absorbance, which corresponds to the absorbance per mg/L of DOC, is a useful tool for rapidly assessing the "humic/non-humic nature" of a water. Some specific absorbances for extracted humic and non-humic fractions are shown in Figure 17.2. Note that humic acid and fulvic acid show the highest SUVA (6.3 and 4.4, respectively). In another study, averages of 10 aquatic humic substances showed SUVA values of 5.8 for the humic acids and 3.6 for the fulvics (Reckhow et al., 1990). Other fractions, especially the hydrophilic acids, show lower SUVA values. For this reason, waters with a high SUVA generally have higher humic contents, and are more amenable to DOC removal by coagulation.
Table 17.3 summarizes some attempts to correlate UV absorbance (254 nm) to DOC for raw waters. Note that the reciprocal of the slopes in Table 17.3 correspond to the specific absorbances in Figure 17.2, and that the average slope (~25) gives a specific absorbance of 0.004/cm or 4/m which is similar to those reported for fulvic acids.
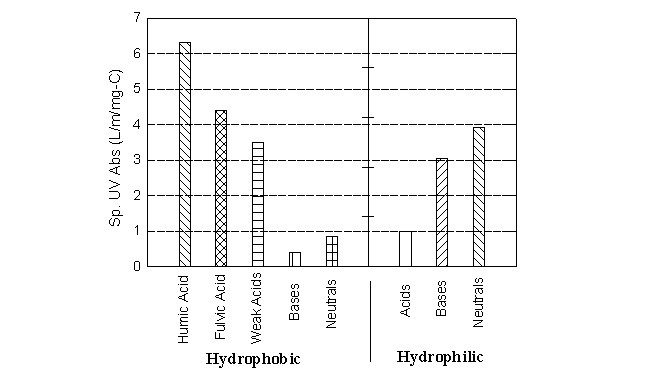
Figure 17.2
Specific UV Absorbance of Eight NOM Fractions from Forge Pond
(After Reckhow et al., 1993)
Table 17.3
UV Absorbance (254 nm) to DOC Regression Equations+
|
Water |
Slope |
Intercept |
r |
Reference |
|
Tjeukemeer Lake |
24.7* |
2.7 |
0.925 |
De Haan et al., 1982 |
|
Grasse River |
19.8 |
0.65 |
0.93 |
Edzwald et al., 1985 |
|
Glenmore Reservoir |
28.1 |
-0.3 |
0.71 |
Edzwald et al., 1985 |
|
|
24.1 |
2.2 |
0.96 |
Smart et al., 1976 |
|
N.C. Surface Wat. |
29.1 |
1.44 |
0.83 |
Singer et al., 1982 |
|
Norwegian Lakes |
19.1 |
2.3 |
0.93 |
Vik et al., 1985 |
+Model: DOC (mg/l) = (slope)*(UV absorbance, cm-1 ) + intercept
* Based on absorbance at 250 nm, neutral pH.
b. Methods requiring the Formation of a Chromophore
As discussed obove, most specific chemical analytes do not have large enough absorptivities to make their determinations by direct spectrophotometry practical. However, through a variety of means, one can increase their molar absorptivities. This is most often done through the formation of a chromophore, a chemical structure that imparts a visible color to a solution. By far the most common group of reactions that is used to form chromophores for spectrophotometric analysis are the complexation reactions (see Table 17.4). Often extractions into organic solvents or redox reactions are needed to improve selectivity (i.e., remove interferences) or sensitivity (i.e., lower detection limit). Other colorimetric methods are based largely on redox reactions (see Table 17.5). This is especially true of analytes that are, themselves, reductants or oxidants (e.g., chlorine). Another class of colorimetric methods relies on the catalysis of an observeable reaction by the analyte (Table 17.6). Here the rate of reaction must be directly proportional to the analyte (catalyst) concentration. These are potentially very sensitive methods. Finally, Table 17.7 lists a number of methods that employ coupling reactions, simple substitutions, or incompletely characterized reactions.
Table 17.4
Colorimetric Methods Based
on the Formation of a Complex
|
Analyte |
Complexing
Metal or Ligand |
Additional
Treatment |
Wavelength |
|
Al |
Eriochrome cyanine R dye |
|
535 nm |
|
Be |
Aluminon (aurintricarboxylic acid ammonium salt) |
|
515 nm |
|
Cd |
dithizone (diphenylthiocarbazone) |
post-extraction (CHCl3) |
518 nm |
|
Cr(VI) |
diphenylcarbazide |
|
540 nm |
|
Cu |
neocuproine (2,9,-dimethyl-1,10-phenanthroline) |
post-extraction(CHCl3& CH3OH) |
457 nm |
|
Cu |
bathocuproine disulfonate |
|
484 nm |
|
Fe |
1,10-phenanthroline |
pre-reduction (hydroxylamine) |
|
|
Pb |
dithizone |
pre-extraction (CCl4) |
520 nm |
|
Hg |
dithizone |
pre-extraction (CHCl3) |
490 nm |
|
Ni |
dimethylglyoxime |
pre-extraction (CHCl3,then H2O) |
445 nm |
|
Se |
diaminobenzidine |
pre-oxidation, pre-reduction post-extraction (C6H5CH3) |
420 nm |
|
Zn |
dithizone |
pre-extraction (CCl4) |
535/620 nm |
|
Zn |
zincon |
|
620 nm |
|
As |
silver diethyldithiocarbamate |
pre-reduction (Zn) |
535 nm |
|
B |
curcumin |
|
540 nm |
|
B |
carmine |
|
585 nm |
|
SCN |
Fe(+III) |
|
460 nm |
|
F |
SPADNS |
reaction (zirconium) |
570 nm |
|
PO4 |
Mo |
post-reduction (SnCl2) |
690 nm |
|
PO4 |
Mo |
post-reduction (ascorbic acid) |
880 nm |
|
Silica |
Mo |
|
410 nm |
|
SO4 |
methylythymol Blue |
pre-precipitation (Ba), chelation of excess Ba & detn of excess ligand |
460 nm |
Table 17.5
Colorimetric Methods Based on Redox Processes
|
Analyte |
Oxidant
or Reductant |
Additional
Treatment |
Wavelength |
|
Mn |
persulfate or periodate (to Mn(+VII)) |
|
525 nm |
|
K |
dichromate |
pre-precipitation (sodium cobaltinitrite) & oxdn of excess |
425 nm |
|
Br(-I) |
chloramine-T (to Br(+1)) |
post-reaction (bromination of phenol red) |
590 nm |
|
Cl(+I) & ClO2 |
DPD |
|
515 nm |
|
CN |
chloramine-T (to CNCl) |
post-reaction (pyridine- barbituric acid) |
578 nm |
|
I(-I,+I) |
Leuco Crystal Violet |
pre-oxidation (potassium peroxymonosulfate) |
592 nm |
|
NH3 |
HOCl |
post-reaction (phenol) (to indophenol, phenate method) |
630 nm |
|
O3 |
Indigo Trisulfonate |
|
600 nm |
|
Tannins & Lignins |
tungstophosphoric & molybdophosphoric acids |
|
700 nm |
Table 17.6
Colorimetric Methods Based
on Catalysis
|
Analyte |
Reaction |
Additional
Treatment |
Wavelength |
|
V |
oxidation of gallic acid by persulfate |
|
415 nm |
|
I(-I) |
reduction of Ce(+IV) by arsenious acid |
remaining Ce(+IV) reduced by Fe(+II), residual measured at |
410 nm |
Table 17.7
Colorimetric Methods Based
on Miscellaneous Reactions
|
Analyte |
Reactions/Reactants |
Additional
Treatment |
Wavelength |
|
NH3 |
KI + HgI2 |
|
410 nm |
|
NO3/NO2 |
diazotization with sulfanilamide then coupling with N-(1-naphthyl) -ethylenediamine) |
pre-reduction (Cd) (to nitrite, for nitrate analysis only) |
543 nm |
|
NO3 |
Chromotripic Acid |
|
410 nm |
|
S(-II) |
S(-II), FeCl3 & dimethyl-p- phenylenedeamine (forms methylene blue) |
|
664 nm |
|
Phenols |
4-aminoantipyrine, potassium ferricyanide |
post-extraction (CHCl3) |
460 nm |
b. Measurement of Al and Fe
Iron and aluminum are polyvalent metals that are used as coagulants in drinking water treatment. They are also present in natural waters at usually low concentrations. In properly operating drinking water treatment plants, metal coagulants are well removed by sedimentation or filtration. However, extremes of pH, incorrect dosing, or poor hydraulics may result in the breakthrough of high levels of residual iron or aluminum in the distribution system. This is undesirable for several reasons. First these hydrolysing metals may continue to slowly precipitate far downstream of filtration. This will cause hydraulic and water quality problems in any engineered systems that does not have provisions for sludge removal (i.e., clearwells, water mains, etc.). Iron may actually impart a metallic taste at high concentrations, and it is well known to stain plumbing fixtures and laundry. Under certain circumstances iron residuals can support the growth of unwanted bacteria. In the U.S. a secondary maximum contaminant level has been set for iron at 300 g/L (based on aesthetics). The corresponding European recommended standard is 50 g/L, with an MCL of 200 g/L. High concentrations of aluminum have been linked to encepalopathy in kidney dialysis patients. There is also some weak evidence that it may be associated with Alzheimer's Disease as well. In Europe, residual aluminum concentrations in drinking water are limited to 200 g/L, and the recommended limit is 50 g/L. A primary drinking water standard (most commonly 50 g/L) is currently being discussed for the U.S.
Aluminum and iron may be determined in aqueous solution together by the simultaneous formation of of two separate colored complexes; Al-ferron, and Fe-phenanthroline (Davenport, 1949). The formation of an Fe-phenanthroline complex must be preceeded by two steps. First iron hydroxides must be dissolved with acid (equation 17.15a), then the iron must be reduced to the ferrous state with hydroxylamine (equation 17.15b).
Fe(OH)3 + 3HCl ------> Fe+3 + 3H2O + 3Cl- (17.15a)
4 Fe+3 + 2 NH2OH ------> 4 Fe+2 + N2O + H2O + 4H+ (17.15b)
The
ferrous-iron then forms a strongly-colored complex with three molecules of
1,10-phenanthroline. Binding occurs at
the heterocyclic nitrogens. This
complex is reported to have a molar absorptivity (![]() )
of 11,100 M-1cm-1 at max = 508 nm (i.e.,
orange-red). The intense color is
attributed to charge transfer of an electron from Fe(II) to a vacant * orbital on the
phenanthroline. Such a transition
cannot occur with Fe(III). As a result,
this latter complex only possesses a slight bluish color due to the weaker
ligand-field transition phenomena.
)
of 11,100 M-1cm-1 at max = 508 nm (i.e.,
orange-red). The intense color is
attributed to charge transfer of an electron from Fe(II) to a vacant * orbital on the
phenanthroline. Such a transition
cannot occur with Fe(III). As a result,
this latter complex only possesses a slight bluish color due to the weaker
ligand-field transition phenomena.
Aluminum forms a colored complex with several hydroxyquinoline derivatives. One of these ligands, 8-hydroxy-7-iodo-5-quinolinesulfonic acid (or Ferron; abbreviated as "F" below), gives an absorbance maximum at about 370 nm. This reaction is most sensitive at pH 5.5, and it is subject to interference from iron. However iron interference can be conveniently removed by simultaneous complexation with 1,10-phenanthroline (abbreviated as "P" below). In this way, a combined ferron/phenanthroline reagent allows the simultaneous determination of iron and aluminum when absorbances at 370 nm and 520 nm are recorded. For example, the overall absorbance measured at either of these two wavelengths can be broken down as follows:
![]() (17.16)
(17.16)
where:
![]() =
the Total absorbance
of a sample or standard at wavelength "x"; i.e. the absorbance that
you directly measure with a spectrophotometer.
=
the Total absorbance
of a sample or standard at wavelength "x"; i.e. the absorbance that
you directly measure with a spectrophotometer.
![]() = the absorbance of the sample or standard
prior to addition of complexing reagents (i.e., initial sample
absorbance) at wavelength "x"
= the absorbance of the sample or standard
prior to addition of complexing reagents (i.e., initial sample
absorbance) at wavelength "x"
![]() =
the fraction of the total absorbance that is due to free, un-complexed Ferron at wavelength
"x"
=
the fraction of the total absorbance that is due to free, un-complexed Ferron at wavelength
"x"
![]() =
the fraction of the total absorbance that is due to free, un-complexed Phenanthroline at wavelength
"x"
=
the fraction of the total absorbance that is due to free, un-complexed Phenanthroline at wavelength
"x"
![]() = the fraction of the total absorbance that
is due to Al-Ferron complex
= the fraction of the total absorbance that
is due to Al-Ferron complex
![]() = the fraction of the total absorbance that
is due to Fe-Phenanthroline
complex
= the fraction of the total absorbance that
is due to Fe-Phenanthroline
complex
Invoking Beer's Law and assuming that all aluminum and iron are completely complexed, we presume that:
![]() (17.17)
(17.17)
![]() (17.18)
(17.18)
![]() (17.19)
(17.19)
![]() (17.20)
(17.20)
where
![]() is the absorptivity (usually in: abs
units/mg/L) of substance "y" at wavelength "x". The free ligand concentrations are:
is the absorptivity (usually in: abs
units/mg/L) of substance "y" at wavelength "x". The free ligand concentrations are:
![]() (17.21a)
(17.21a)
![]() (17.21b)
(17.21b)
where "n" and "m" are stoichiometric factors that relate the amount of ligand bound per unit of metal. Now combining equations 17.16 through 17.21b one gets:
![]() (17.22)
(17.22)
and this reduces to:
![]() (17.23)
(17.23)
And
if we define the absorbance of the added ligands in their free state (i.e. initial ligands) as ![]() ,
,
![]() (17.24)
(17.24)
we get:
![]() (17.25)
(17.25)
Now we know that aluminum can be best measured near the absorbance maximum for the aluminum-ferron complex (370nm), and iron is best quantified at a wavelength near the iron-phenanthroline maximum (520nm). From this we can used equation 17.25 to formulate an expression for Fe and Al concentration:
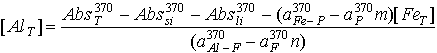 (17.26)
(17.26)
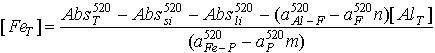 (17.27)
(17.27)
The first term of both equations 17.26 and 17.27 (AbsT) is simply the final absorbance of the samples or standards after treatment with the ferron-phenanthroline reagent. The second term (Abssi) is just the absorbance of the samples before anything is done to them. The third term (Absli) is obtained from the intercept of the standard curves, and the constant parts of the last two terms are determined from the slopes of these standard curves.
c. Ammonia-Nitrogen: The Phenate Method
Ammonia nitrogen may be determined by reaction with phenol and chlorine which gives a new highly colored condensation product, indophenol (Bolleter et al., 1961). The reaction is thought to occur through the formation of monochloramine (equation 17.28). For quantitative formation of monochloramine, the pH must be around 6.5 to 7.0.
NH3 + OCl- NH2Cl + OH- (17.28)
Then this powerful electrophile attacks the anionic phenate to give a quinonechloramine (17.29). This intermediate continues to react with phenate forming the highly-conjugated indophenol (17.30). Manganous sulfate is added as a catalyst.
![]() (17.29)
(17.29)
![]() (17.30)
(17.30)
The color of this final product is quite pH-dependent, yellow at low pH, and blue at high. The blue color is most intense at pH 9.9-10.0.
Procedure
1. To 10 mL of sample in a 100-mL beaker, add 10 mL of high-purity water and 2 drops (~0.1 mL) of manganous sulfate solution.
2. Place on a magnetic stirrer and add 1 mL conc. HOCl solution, followed immediately by the dropwise addition of 1.2 mL phenate reagent. Stir vigorously during the addition of the reagents.
3. Wait 10 min after addition of the reagents, then measure the absorbance at 630 nm.
4. Repeat steps 1-3 for all samples along with a set of 4 standard solutions prepared from the 25 mg/L ammonia solution. The concentrations you choose for the standard solutions should be properly spaced such that the unknowns all fall between the highest and lowest standard.
Reagents
1. Conc. HOCl solution: Dilute 20 ml of the 5% NaOCl stock to 100 mL. Adjust pH to 6.5 - 7.0 with HCl.
2. Manganous sulfate solution (0.006 N): Dissolve 50 mg monohydrate manganous sulfate in 100 mL distilled water.
3. Phenate reagent: Dissolve 2.5 g NaOH and 10 g phenol in 100 mL distilled water.
d. Nitrite-Nitrogen
Nitrite can be measured easily and with good sensitivity by a coupling reaction known as diazotization. Under acidic conditions, nitrite ions and aromatic amines can form reactive diazonium salts. In the test commonly employed for nitrite, the aromatic amine used is sulfanilamide. This forms p-diazobenzenesulfonamide (equation 17.31).
![]() (17.31)
(17.31)
To improve the intensity of the absorbance band, this is reacted with N-(1-naphthyl)ethylenediamine to form a reddish purple azo dye, p-benzenesulfonamide azonaphthylethylenediamine (equation 17.32).
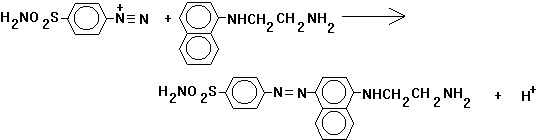 (17.32)
(17.32)
Absorbance of this azo dye is measured at 543 nm. It obeys Beer's law up to 180 g-N/L. This method requires the use of nitrite-free dilution water and accurate nitrite standards. If its not certain that distilled water is nitrite-free, it can be treated with a small amound of potassium permanganate. This common oxidizing agent converts nitrite to nitrate. Residual permanganate can be removed by fractional distillation of the water, discarding any pink distillate. Because nitrite is so easily oxidized, even fresh solutions must be standardized. This is done by oxidation with a standard permanganate solution and back titration with a standard reducing agent (oxalate or ferrous ammonium sulfate).
Procedure
1. To 50 mL of sample in a 100 mL beaker, add 2 mL of the color reagent and mix..
2. Wait 10 min after addition of the reagents, then measure the absorbance at 543 nm. If the absorbance is greater than that measured for the 0.025 mg/L standard, dilute the original sample and repeat steps 1-2.
3. Repeat steps 1-2 for all samples along with three standard solutions prepared from the 250 mg/L nitrite-N solution.
Reagents
1. Color Reagent: Place about 800 mL of distilled water to a 1-liter volumetric flask. To this slowly add 100 mL of 85% phosphoric acid and then 10 g sulfanilamide. Once the sulfanilamide is completely dissolved, add 1 g N-(1-naphthyl)-ethylenediamine dihydrochloride and dissolve. Dilute to 1 liter. This reagent must be stored in a dark bottle in a refrigerator. It can be used for 1 month.
2. Nitrite Standard (250 mg/L as N) Dissolve 1.232 g NaNO2 in 1 liter of distilled water. Add 1 mL chloroform as a preservative. Standardize with permanganate and oxalate or ferrous ammonium sulfate.
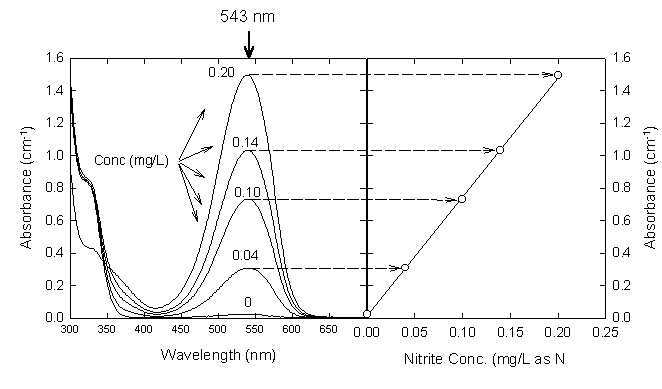
Figure 17.3
Nitrite Standard Curve
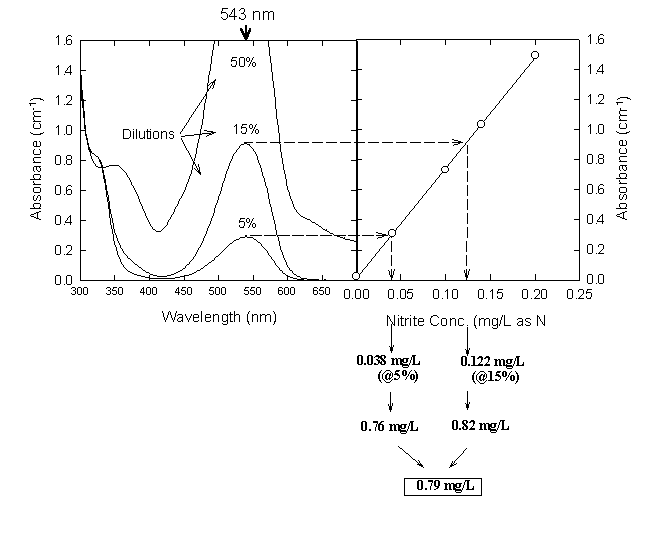
Figure 17.4
Determination of Nitrite in an Unknown from Several Dilutions