CHAPTER XIV

SAMPLE PREPARATION

A. Introduction

Most analytical techniques require some type of pre-treatment of the sample prior to final measurement of the analyte. This is done for one or more of the following reasons:

1. Improve method sensitivity by:

a. concentrating the analyte

b. changing the chemical nature of the analyte to a form which gives a greater response (e.g, derivatization, complexation)

2. Remove interfering substances (i.e., isolation)

3. Transferring the analyte to a solvent or phase (e.g., gas) that is compatible with the analytical method

These sample preparatory techniques have become especially important since the widespread use of gas chromatography for trace organic analysis. Sample pretreatment techniques may be classified according to physical and chemical methods:

A. Pysical Pretreatment

1. Concentration

a. Phase Change

- freeze concentration, freeze drying, vacuum distillation, atmospheric pressure distillation

b. Membrane Processes

- reverse osmosis, ultrafiltration, dialysis

2. Isolation

a. Gas Stripping/Gas Transfer

- purge & trap, closed loop stripping, headspace analysis

b. Solvent Extraction (SE)

- Liquid-Liquid extraction (LLE), Soxhlet extraction, Sonication extraction

c. Solid-Phase Extraction (SPE) or adsorption

- Ion exchange resins, hydrophbic resins (e.g., XAD-4), activated carbon, polar adsorbents (e.g., alumina, florisil, silica gel)

3. Change of Solvent/Phase

a. Solid to Liquid

- (see solvent extraction [2b])

b. Liquid to Liquid

- solvent exchange

B. Chemical Pretreatment

1. Derivatization

- Alkylation (e.g., diazomethane), Silylation, detector-specific derivatives (e.g., pentafluorobenzyl bromide)

2. Digestion

3. Complexation

4. Reduction

- Sulfite, thiosulfate, arsenite, citrate, ammonia

The concentration techniques (A1) and some of the derivatization or complexation techniques (B1,2) are aimed at improving method sensitivity. The isolation methods (A2) and chemical reduction (B3( are primarily aimed at removing interferents. Although, they often are designed to achieve some sample concentration as well. Finally, a change of solvent or phase (A3) is sometimes needed due to incompatabilities between the sample and the analytical method.

B. Physical Pretreatment Methods

1. Concentration

Sample concentration techniques are primarily aimed at improving method sensitivity. A good concentration technique is one that:

aviods chemically-altering the sample

avoids excessive loss of analyte

It should be remembered that indiscriminant sample concentration leads to a build-up of all constituents, analytes and potential interferents.

a. Phase Change

Freeze Concentration is a technique where a sample is placed in a cylindrical refrigerated chamber with constant stirring. The sample slowly freezes starting at the outside perimeter. In theory, as the water freezes, it crystallizes, excluding all solutes. In time the solutes are forced into smaller and smaller volumes of still liquid water in the center of the cylinder. Eventually the concentrated liquid sample is removed.

b. Membrane Processes

2. Isolation

a. Solvent Extraction

Solvent Extraction is a simple and widely-used technique that can isolate an analyte from potential interferents and achieve a substantial degree of sample concentration as well. Sometimes solvent extraction is used to change the phase of a sample (e.g., from solid to liquid, from one solvent to another). Batch solvent extraction has traditionally employed a separatory funnel. However modern microextraction methods often use small septum-capped vials. One advantage of the latter is the reduced amount of solvent that must be disposed of.

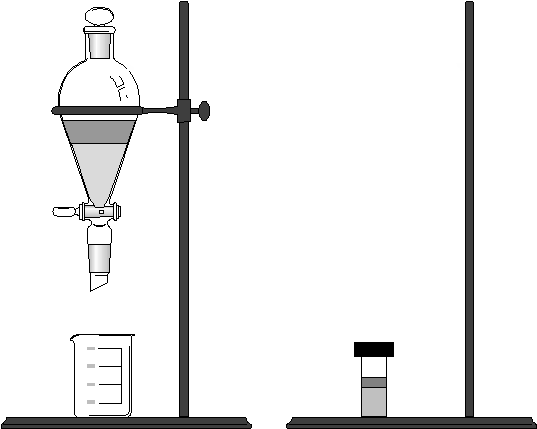
Separatory Funnel Small Vial

Figure 14.xx

Macro and Micro Extraction Labware

Extraction of most substances into a solvent can be characterized by a partition coefficient, K_D. For liquid-liquid extractions involving an aqueous sample, this is simply equal to the concentration of the solute in the solvent phase, C_s, divided by its equilibrium concentration in the aqueous phase, C_w.

K_D = C_s/C_w (14.1)

These partition coefficients are dependent on the particular solute of interest, the nature of the solvent, the ionic strength of the water phase, and the temperature. pH can also play an important role, because it may result in changes in the chemical form of the solute, from charged to uncharged, or the reverse. In general, charged species have extremely low partition coefficients.

A useful measure of the effectiveness of an extraction is the fractional extraction efficiency, ƒ_e. By definition, this value is equal to the mass of the solute in the solvent phase, m_s, divided by the total mass in both phases.

(14.2)

Given the simple partition model for extraction, one can easily calculate fractional extraction efficiencies from equation 14.2. First, an alternative form for the definition of fractional efficiency is formulated by substituting concentration times phase volume (V) for solute mass.

(14.3)

and rearranging, one gets:

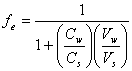(14.4)

and combining with equation 14.1 gives:

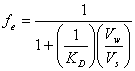(14.5)

Example 14.1: Chloroform has a pentane:water partition coefficient of 50 at 20°C. What is the fractional extraction efficiency for a system consisting of 1 liter of aqueous solution and

a. 50 mL pentane?

b. 25 mL pentane, followed by phase separation, then a second 25 mL volume of pentane?

a)

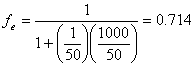(14.E1)

b.) for each of the two serial extractions:

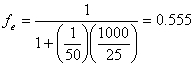(14.E2)

however, for the second extraction, the concentration is reduced to 1-ƒ_{e of the original, so that the overall, two-step serial extraction efficiency, ƒ2e, is:}

(14.E3)

or 80.2% (14.E4)

The concentration of a solute in each phase after extraction can be determined from equation 14.1 and a mass balance, before and after extraction:

(14.6)

where C_wi is the initial concentration of the solute in the aqueous phase prior to extraction. Combining this with equation 14.1 and rearranging, one gets:

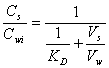(14.7)

Example 14.2: For each of the two cases in example 14.1, calculate the ratio of the chloroform concentration in the final pentane extract to the initial aqueous phase concentration.

a.)

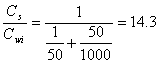(14.E5)

b.) First extraction:

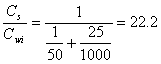(14.E6)

Second extraction:

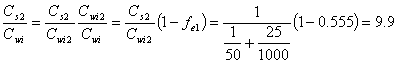(14.E7)

It is evident from equation 14.5 that extraction efficiency must increase with increasing solvent to water ratio. This means that larger solvent volumes will permit higher percent extractions and greater analyte recovery. In addition, high extraction efficiencies are usually accompanied by good reproducibility. This is better illustrated by rearranging equation 14.5 to get 14.8, and the two limiting cases, 14.9 and 14.10

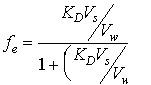(14.8)

(14.9)

(14.10)

One of the principal sources of error in LLE is the variability that can exist in ƒ_e due to different K_D values under different conditions. The partition coefficient may be very sensitive to changes in temperature, and differences in sample matrix (ionic strength, ligands, etc.). For the sake of illustration, lets assume that a 30% variability may exist in the K_D of an analyte over a wide range of samples. The resulting variability in ƒ_e will then be about 30% as well when the extraction efficiency is low (i.e., the term, K_DV_s/V_w is small). When this is the case, equation 14.8 reduces to equation 14.9 and the relative uncertainty in ƒ_e is equal to the relative uncertainty in K_D (assuming the volumes can be measured quite accurately). In the other extreme (equation 14.10), uncertainty in ƒ_e is no longer dependent on K_D, and it approaches zero (as ƒ_e1)

Gas Stripping or Purge-and-Trap

Theoretical Background

There are a variety of extraction techniques that rely on a liquid-to-gas phase transfer. When the compounds of interest are volatile, this technique can be used to both concentrate the analytes and leave behind non-volatile interferents. Whether or not an analyte is volatile depends on its affinity for water and the dissolved phase. This affinity is quantified by Henry's Law.

(14.11)

where H_i^*is the compound-specific Henry's Law Constant (in atm), and p_i is the partial pressure (in atm) of compound "i" that is in equilibrium with an aqueous phase concentration correspoding to a mole fraction, x_i. The mole fraction is the ratio of the moles of compound of interest to the total number of moles of water and all other constituents.

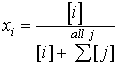(14.12)

Due to non-idealities, Henry's Law becomes inaccurate and cannot be used at mole fractions above 0.05. In dilute solutions and most natural waters, the mole fraction is simply equal to the molar concentration divided by 55.6, which is the number of moles of water in a liter volume at 25C. Under these conditions, the more familiar molar-based Henry's Law Constant, H_i, is used (units: atm-L/mole):

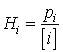(14.13)

and:

(14.14)

A sampling of Henry's Law Constants appears in the following two tables. Note that as the constants increase in value the become more volatile or easily stripped from water. For a given homologous series (e.g., the alkanes), volatility increases with increasing length of the alkyl chain. Double bonds render a compound more soluble in water (i.e. of lower volatility), and aromatics are especially soluble.

Table 14.1

Some Henry's Law Constants for Inorganic Substances (25C)

(from Stumm & Morgan, 1981)

Compound	H (atm-L/mole)
Nitrogen	1560
Hydrogen	1230
Carbon Monoxide	1047
Oxygen	793
Carbon Dioxide	29.4
Mercury	11.5
Hydrogen Sulfide	9.8
Sulfur Dioxide	0.81
Ammonia	0.017

Table 14.2

Some Henry's Law Constants for Organic Compounds (25C)

Compound	H (atm-L/mole)	Compound	H (atm-L/mole)
Methane	67420	Benzene	5.50.25
Ethane	50611	Toluene	6.70.35
Propane	71624	Ethylbenzene	8.00.7
n-Butane	96040	p-Xylene	7.10.8
n-Pentane	1250100	m-Xylene	7.01.0
n-Hexane	1700250	o-Xylene	5.00.6
n-Heptane	2300500	Naphthalene	0.430.04
n-Octane	3000500	Anthracene	0.0600.03
n-Nonane	50002000	Pyrene	0.0120.02
n-Decane	70003000	Chloroform	3.80.3
Ethene	21720	Carbon Tetrachloride	204
Propene	21330	1,1,1-Trichloroethane	280.4
1-Butene	75040	Tetrachloroethylene	234
1-Pentene	40320	Bromoform	0.620.06
1-Hexene	41810	DDT	0.00320.0002

As stated previously, Henry's Law breaks down at elevated mole fractions (e.g., x_i>0.05) when solute-solute interactions become important. Therefore, when working with organic liquids, rather than dilute aqueous solutions, Raoult's Law must be used. This holds that the partial pressure of a consituent "i" is equal to its mole fraction multiplied by the partial pressure of pure "i", p_i^o.

(14.15)

Practical Aspects

For purge and trap to be successful, sufficient opportunity must be provided for the analyte to become transported from the aqueous phase to a carrier gas phase, then back again to a separate trapping phase. Efficient trapping relies on a large affinity of the analyte for the trapping substance. Sometimes trapping is combined with reagents which produce a rapid chemical reaction simultaneous with the phase transfer. The trapping efficiency in these cases increases in proportion to the rate of this reaction (e.g., Danckwerts, 1970). Thus, when trapping is combined with reaction, the overall efficiency may depend on the specifics of the reaction kinetics, as well as the affinity of the analyte for the trapping phase.

Compounds with a high Henry's law constant are easily purged. By a simple mass balance, one can calculate the maximum purging efficiency (ƒ_p) as a function of time (t) from equation 14.16.

(14.16)

This is related to the carrier gas flow rate (G), and the voluem of aqueous sample (V_w). The term, Gt/V_w is just the gas/liquid volumetric ratio (R_gl). If this is substituted into equation 14.16, one gets:

(14.17)

In practice the purging efficiencies will often be lower than calculated from equations 14.16 or 14.17. This because we implicitly made two assumptions in getting these equations:

1. The aqueous phase is completely mixed

2. Sufficient contact between the gas and liquid exists that by the time the bubbles reach the surface, they are saturated with the analyte.

For small vessels, the first may be approximately true. However, when the second assumption is not met, purging efficiency will decline. On the other hand, if the sample contains a high ionic strength, the actual Henry's law constant may be much larger than the literature value (which is often evaluted at low ionic strength), adn the observed purging efficiency may be much larger than one would calculate.

The degree of aqueous mixing and gas-liquid interaction (i.e., the validity of the above assumptions) will depend on the geometry of the purging vessel, and the diffusion rate of the analyte. Such characteristics must be evaluated empirically. The standard US EPA protocol for purge and trap analysis of most volatile organic compounds employs a long, narrow purging vessel with a porous diffuser covering the entire bottom. The purging conditions are as follows:

5 mL sample volume

ambient temperature

40 mL/min gas flow rate

11 min purge time

This gives as gas/liquid volumetric ratio (R_gl) of 88. This is well established as a reliable and robust procedure for the THMs. It is quick, uses a small sample volume, and does not require sample heatin. Also, it delivers sufficient analyte so that when coupled with electron dcapture detection, the limit of detection is about 0.5 µg/L. Data from Bellar and Lichtenbert (1974) suggest that this protocol will give maximum theoretical results at gas flow rates equal to 4 liquid volumes per minute (Table 14.3). However, at lower flow rates, the purging efficiency may be less than optimal.

Table 14.3

Purging Efficiency of Chloroform Using the USEPA Sparger

(From Bellar & Lichtenberg, 1974)

Specific Purge Flow	Gas/Liquid Ratio	Purge Efficiency
(gas flow/liquid flow)	(Rgl)	Measured	Calculated^*
2.6 min^-1	1.3	18%	6%
	17	93%	71%
	29	99%	100%
4 min^-1	4	45%	46%
	20	99%	100%

^*from equation 14.17

In principle, method detection limit could be improved by using a larger sparger with a larger sample volume. Although, potential difficulties in scale-up from the USEPA procedure must be carefully considered, the data of Pellizzari et al. (1985) are encouraging in this regard. They were able to obtain 97±0.8% purging efficiency of chloroform (1.8 µg/L concentration) from 200 mL samples with a gas/liquid volumetric ratio of only 2.5. They used a helium flow rate of 20 mL/min for 25 min at 25°C. They also saturated the aqueous phase with Na₂SO₄. Such high recoveries at low gas/liquid ratios suggests that by use of the salt they were able to increase the Henry's law constant by an order of magnitude.

In addition, Pellizzari et al. (1985) examined three purging vessels of different geometry: (1) a simpel scale-up of the USEPA sharger; (2) a 1000-mL erlenmeyer flask with an open tube releasing the gas 4-cm above the water surface (the water forms a shallow layer on the bottom, and is agitated by means of a magnetic stirrer)' and (3) a 125-mL erlenmeyer flask with a full-bottom fritted disk (no magnetic stirrer). Tests with a semi-volatile compound showed the first to be slightly superior, although the differences may not have been significant. Pellizzari et al. (1985) also found that with a fixed sample size (i.e., 200 mL) and temperature (25°C), only the purge gas volume and ionic strength were important in determining purge efficiency. This was demonstrated over a range of gas flows of 10-100 mL/min and purging times of 36-360 min.

Acid Digestion

Sample is acidified with nitric acid for preservation. At the start of analysis, more acid is added and the sample is heated to 90-95°C and reduced in volume. If the sample is allowed to boil, substantial volatilization of antimony may result. The digestate is then filtered, diluted to a known volume and analyzed (EPA method 3005). This gives the total recoverable metals. Some metal complexes will survive this procedure. For dissolved metals, sample must be first filtered (0.5 µm pore). This procedure is rather mild, and is only recommended for aqueous samples.

Sample is acidified with nitric acid and refluxed in a covered Griffin beaker. As the volume is reduced, more nitric acid is added until the color stablizes. Next it is refluxed with HCl, and finally brought up to a known volume with this acid. After cooling, the sample is now ready for analysis (EPA method 3010). If the sample is to be anayzed by graphite furnace atomic absorption spectroscopy, the final step involving HCl must be skipped (EPA method 3020). Otherwise the use of HCl would interfere with the sample atomization step. These methods are more vigorous than the previous. Higher temperatures will result in loss of antimony, and use of HCl will cause silver to precipitate, so it cannot be used for these two metals. These methods may be used for analysis of wastes containing suspended solids.

If the samples are in the form of sludges, sediments and soils, an even more rigorous digestion must be used. Instead of just adding nitric acid, hydrogen peroxide is added as well. The sample is then refluxed as before, with a final reflux in HCl (EPA methos 3050).

Literature Cited.

Bellar, T.A. and J.J. Lichtenberg (1974) "Determination of Volatile Organics at Microgram-per-liter Levels by Gas Chromatography," J. Am. Wat. Wrks. Assn., 66:12:739-744.

Danckwerts, P.V. (1970) Gas-Liquid Reactions, McGraw-Hill, Inc., New York

Mackay, D. and W.Y. Shiu (1981) "Critical Review of Henry's Law Constants for Chemcials of Environmental Interest," J. Phys. Chem Ref. Data, 10:4:1175-1199.

Pellizzari, E.D., L.S. Sheldon, J.T. Bursey, W. Hargrove, L.C. Michael, and R.A. Zwidinger (1985) Master Analytical Scheme for Organic Compounds in Water, part I: Experimental Report. EPA/4-85-007a. NTIS, Washington.

Stumm, W. and J.J. Morgan (1981) Aquatic Chemistry, 2nd Ed., John Wiley & Sons Publ., New York.