|
CEE 370 |
November 16, 2006 |
Exam #2
Closed Book, two sheets of notes allowed
Please answer any combination of the following 9 questions such that the total potential is 100%. Show all work. Be neat, and box-in your answer.
1. Short answer (25 points)
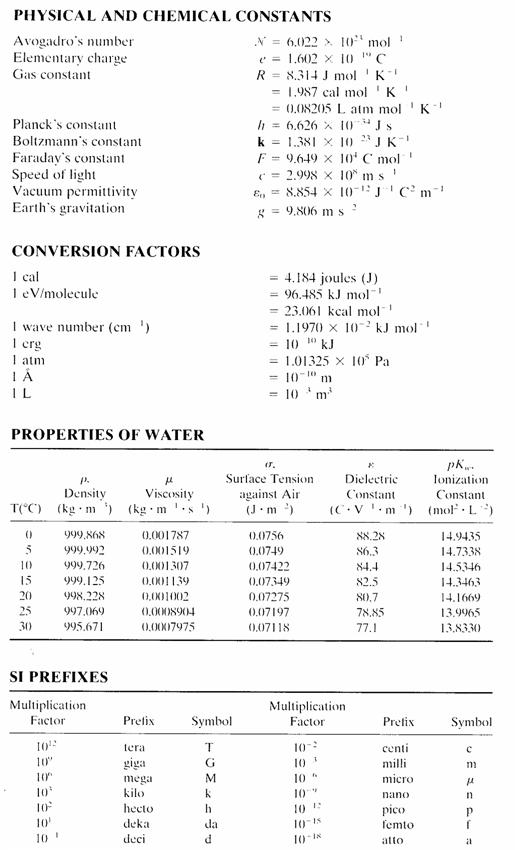
a. Sketch a typical growth curve for a bacterial population in a batch culture, and describe the various phases (5 points)
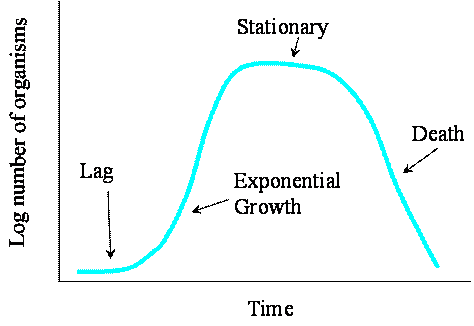
b. Sketch 3 different population growth models, list their names and briefly describe how they differ. (5 points)
See book or class overheads. Models include: linear, exponential, logistic, Monod
c. What are the factors that can limit bacterial growth? Explain. (5 points)
Carrying capacity, which might include such factors as population density, presence of toxins, availability of food (electron donor, and carbon source), temperature, pH, light energy (for phototrophs), disease.
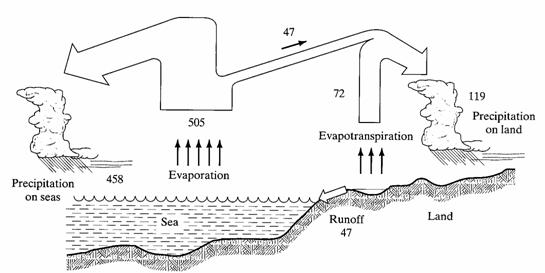
d. Describe the global water balance in qualitative terms. Sketch a diagram showing the various forms of water in the environment and routes of movement. It’s not necessary that you show exact flux values (5 points).
e. What are genomics and proteonomics? (5 points)
2. Groundwater and contaminant flow (25
points)
Two groundwater wells are located 105 m apart within the same aquifer. Well #1 has a water level at 557 ft above mean sea level. The second well’s water level is 645 ft above mean sea level. The mean hydraulic conductivity in this aquifer is 0.12 m/day, and the porosity is 0.55. How long will it take the water to travel from Well #2 to Well #1?
First determine the Darcy’s velocity between the wells
![]()

Then determine the true velocity between the wells
![]()
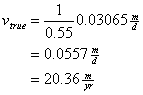
Now determine the time it takes for water to travel between the two wells
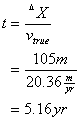
3. Microbial
Growth (25 points)
You’re operating a batch reactor. At the start (time =0) you have 0.33 mg/L of biomass. After five and one-half hours of operation you find that the biomass concentration is 0.44 mg/L. You know that this particular substrate you’re treating is characterized by a half-saturation coefficient of 7.5 mg/L. The starting substrate concentration was 6 mg/L and the final value at 5.5 hours was essentially unchanged.
a. What is the specific growth rate assuming simple exponential growth throughout?
From Equation 5-5:
![]()
![]()
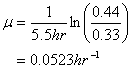
b. What is the maximum specific growth rate for this system?
![]()
so:
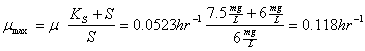
4. Reactor Kinetics #1 (25 points)
You’re using a CMFR to treat an industrial waste containing phenol. Aqueous chlorine reacts with phenol according to second order kinetics (first order in phenol and first order in chlorine). The observed second order rate constant for this reaction is 2.23x103 M-1min-1 at the temperature and pH of the wastewater (25 C, and pH 7.0). To accomplish this removal you’ve designed a CMFR reactor with a volume is 50 m3 and you’ve decided to add aqueous chlorine so that the concentration in the reactor is constant at 0.001 moles/L. If the volumetric flow rate at the inlet and outlet is 5000 m3/day and then inlet phenol concentration is 10-4 moles/L, what will the phenol concentration at the outlet be?
This may be viewed as a pseudo-first order reaction:
![]()
where: k=k2[Chlorine]=2.23x103M-1min-1(0.001M)=2.23min-1=3,210d-1
and now:
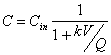
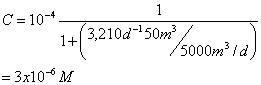
5. True/False. Indicate whether the following statements are true (T) or false (F). (25 points total; 2.5 points each)
|
1. |
T |
PFRs are
always more efficient that CMFRs for 1st order processes |
|
2. |
T |
Chemoheterotrophs
use inorganic chemicals for energy |
|
3. |
F |
Primary
producers include all of the higher animals |
|
4. |
F |
Fick’s
first law describes advective flow |
|
5. |
F |
The NOAEL
is the dose level that causes 100% mortality |
|
6. |
T |
Darcy’s law
describes flow in porous media |
|
7. |
F |
Evapotranspiration
is the process by which water moves from groundwater to a river |
|
8. |
F |
Rotifers
are a form of algae |
|
9. |
T |
Protozoa
can exist in a cyst form |
|
10. |
T |
Most nitrogenous
BOD is in the form of ammonia or organic amines |
6. BOD and Stream modeling (50 points)
A secondary wastewater treatment plant treats a flow of 0.5 m3/s of raw sewage prior to discharge to a river. The river immediately downstream of the outfall has a winter season flow of 2.0 m3/s at a temperature of 5 °C and a summer season flow of 1.0 m3/s at a temperature of 20 °C. Just upstream of the wastewater discharge the river is typically 90% saturated with dissolved oxygen (i.e., DOr = 0.9 DOsat) and has no BOD. The treated wastewater has dissolved oxygen levels of 4.0 mg/L in winter and 2.0 mg/L in summer. The reaeration constant for the river is 0.25 day-1 throughout the year. Assume complete mixing of the wastewater discharge and the river.
A. A 5-day BOD test was conducted at standard temperature (20 °C) on a treated wastewater. To run this test, the analyst used 40 mL of wastewater and 260 mL of dilution water. The initial and final (5 day) DO levels in the 300 mL BOD bottle were 8.0 mg/L and 4.0 mg/L respectively. What is the BOD5 of the (undiluted) treated wastewater (7 points)?
B. If both the first-order BOD bottle constant (k or kb) and the deoxygenation rate constant (kd or k1) at 20 °C are 0.38 day-1, what is the ultimate BOD of the treated wastewater (7 points)?
C. Assuming that the same concentration and characteristics of carbonaceous oxygen demanding waste is in the treated wastewater throughout the year, what is the BOD concentration (L) in the river in the winter at a downstream travel time of two days (13 points)?
D. What is the initial dissolved oxygen deficit in the river at the point of mixing in the summer (6 points)?
E. In the summer the stream velocity is 0.2 m/s. How far downstream (in m) does the minimum dissolved oxygen concentration occur in the summer? What is the value of the minimum dissolved oxygen concentration (17 points)?
No one selected this problem
7. Reactor Kinetics #2 (25 points)
Northampton uses the Mountain Street
Reservoir in Williamsburg Northampton Northampton
For a PFR:
![]()
First let’s calculate the volume of the pipe:
![]()
Next let’s determine the pseudo-first order rate constant, k:
![]()
where:
![]()
now combining:
![]()
This is also equal to 11.4 ppb.
8. Lake Nutrient
Amherst Lake
a. What is the steady state phosphorous concentration (in mg/L) leaving the lake if there are no inputs of P other than the inflow stream?
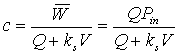

or
0=PinQin-ksVPout-PoutQout
0=(0.030g/m3)(0.8m3/s)-5.79x10-7s-1)(5.6x106m3)Pout-(0.8m3/s)Pout
Pout = 0.0059 mg/L
b. If the maximum desirable in lake phosphorous concentration is 0.015 mg/L, what is the maximum allowable rate of phosphorous input (S, in g/s) due to other sources such as direct runoff?
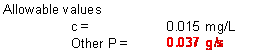
c. What fundamental chemistry principle is the basis for the “limiting nutrient” concept in water quality?
Liebig’s
law of the minimum states that the nutrient in the shortest supply will limit
overall growth. This is determined by
comparing the ratios of the aqueous concentrations with the ratios needed for
biological cells.
d. If the nitrogen concentration in the lake is 0.18 mg/L as N, would the increased P loading in part “b” above lead to increased algal growth in the lake? Prove your answer quantitatively.
The
Redfield ratio is 16 N atoms per 1 P atom.
Therefore when nitrogen is 0.18 mg/L (13 µM), the corresponding P
concentration should be one-sixteenth if both are equally limiting. This would be 0.8 µM, or 0.025 mg/L as
P. Since the actual P concentration is
well below this, it is limiting growth and any increase in P will cause an
increase in growth.
9. Stream modeling, multiple dischargers (50 points)
A nearly pristine river flows through undeveloped land, but along the way it receives two separate point discharges from wastewater treatment plants. Immediately upstream of the first discharge, the river flow is 1.8 m3/s. Assume that the water remains at a constant temperature of 20°C for the purposes of this problem. The upstream water has a BODult of 0.5 mg/L and a dissolved oxygen level of 8.8 mg/L. The depth and width of the river are quite uniform at 1.5 m and 30 m, respectively, throughout its length. Assume complete mixing of the wastewater discharge and the river, and a bed activity coefficient, η, of 0.2.
A. The first WWTP discharges 0.5 m3/s of flow with an ultimate BOD (BODult or L) of 45 mg/L. The BOD bottle rate constant (kb or k) is 0.4375 d-1. The dissolved oxygen of this waste flow is 1.5 mg/L. Calculate the BOD and dissolved oxygen level at a point 5 km downstream (which is immediately upstream of the second WWTP discharge (25 points).
First calculate the velocity after the initial point of mixing:
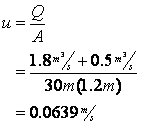
Next determine the deoxygenation rate constant:
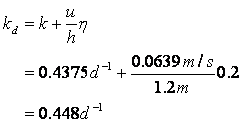
And the reaeration rate:

Now determine the BODu and D at the point of mixing
![]()
And for BOD
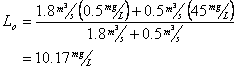
Now for Dissolved oxygen

Which means the initial deficit is: 9.17-7.21 = 1.96 mg/L
The time of travel to 5 km is:
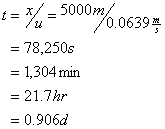
So the downstream ultimate BOD is:
![]()

Now the downstream deficit is determined by the Streeter Phelps equation:
![]()

Which gives a dissolved oxygen concentration of 9.17-3.40 = 5.77 mg/L
B. The second WWTP discharges 5 km downstream of the first one. Its wastewater flow is 0.3 m3/s and it has an ultimate BOD (BODult or L) of 55 mg/L. As with the first wastewater discharge, the BOD bottle rate constant (kb or k) is 0.4375 d-1. The dissolved oxygen of this waste flow is 0.5 mg/L. Calculate the BOD and dissolved oxygen level at a point 5 km downstream of the second WWTP discharge (i.e., 10 km downstream of the first discharge) (25 points).
You need to re-evaluate the “initial” DO and BODs for this second reach of the river
First calculate the velocity after the initial point of mixing:
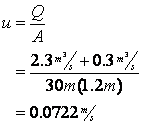
Next determine the deoxygenation rate constant:
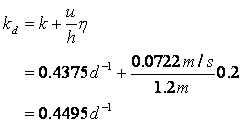
And the reaeration rate:

Now determine the BODu and D at the point of mixing
![]()
And for BOD
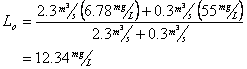
Now for Dissolved oxygen
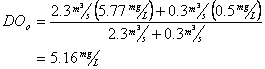
Which means the initial deficit is: 9.17-5.16 = 4.01 mg/L
The time of travel to 5 km is:
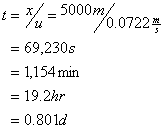
So the downstream ultimate BOD is:
![]()

Now the downstream deficit is determined by the Streeter Phelps equation:
![]()

Which gives a dissolved oxygen concentration of 9.17-4.82 = 4.35 mg/L
Some
additional useful information:
O’Connor Dobbins equation:
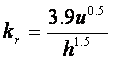
Where: kr (the reaeration coefficient; same as k2 or ka) is in d-1, u (velocity) is in m/s and h (depth) is in m.
Appendix
Selected Chemical Constants
|
Element |
Symbol |
Atomic # |
Atomic Wt. |
|
Electronegativity |
|
|
Aluminum |
Al |
13 |
26.98 |
3 |
1.47 |
|
|
Boron |
B |
5 |
10.81 |
3 |
2.01 |
|
|
Calcium |
Ca |
20 |
40.08 |
2 |
1.04 |
|
|
Carbon |
C |
6 |
12.01 |
2,4 |
2.50 |
|
|
Cerium |
Ce |
58 |
140.12 |
3,4 |
1.06 |
|
|
Helium |
He |
2 |
4.00 |
0 |
|
|
|
Holmiuum |
Ho |
67 |
164.93 |
3 |
1.10 |
|
|
Hydrogen |
H |
1 |
1.01 |
1 |
2.20 |
|
|
Magnesium |
Mg |
12 |
24.31 |
2 |
1.23 |
|
|
Manganese |
Mn |
25 |
54.94 |
2,3,4,6,7 |
1.60 |
|
|
Osmium |
Os |
76 |
190.2 |
2,3,4,8 |
1.52 |
|
|
Oxygen |
O |
8 |
16.00 |
2 |
3.50 |
|
|
Potassium |
K |
19 |
39.10 |
1 |
0.91 |
|
|
Sodium |
Na |
11 |
22.99 |
1 |
1.01 |
|
|
Sulfur |
S |
16 |
32.06 |
2,4,6 |
2.44 |
|
Selected Acidity Constants (Aqueous Solution, 25°C, I = 0)
|
NAME |
FORMULA |
pKa |
|
|
Hydrochloric acid |
HCl = H+ + Cl- |
-3 |
|
|
Sulfuric acid |
H2SO4=
H+ + HSO4- |
-3 |
|
|
Nitric acid |
HNO3 = H+ +
NO3- |
-0 |
|
|
Bisulfate ion |
HSO4-
= H+ + SO4-2 |
2 |
|
|
Phosphoric acid |
H3PO4 =
H+ + H2PO4- |
2.15 |
|
|
Hydrofluoric acid |
HF = H+ + F- |
3.2 |
|
|
Nitrous acid |
HNO2 = H+ + NO2- |
4.5 |
|
|
Acetic acid |
CH3COOH = H+ + CH3COO- |
4.75 |
|
|
Propionic acid |
C2H5COOH
= H+ + C2H5COO- |
4.87 |
|
|
Carbonic acid |
H2CO3 =
H+ + HCO3- |
6.35 |
|
|
Hydrogen sulfide |
H2S = H+ + HS- |
7.02 |
|
|
Dihydrogen phosphate |
H2PO4-
= H+ + HPO4-2 |
7.2 |
|
|
Hypochlorous acid |
HOCl = H+ + OCl- |
7.5 |
|
|
Ammonium ion |
NH4+
= H+ + NH3 |
9.24 |
|
|
Hydrocyanic acid |
HCN = H+ + CN- |
9.3 |
|
|
Phenol |
C6H5OH
= H+ + C6H5O- |
9.9 |
|
|
Bicarbonate ion |
HCO3-
= H+ + CO3-2 |
10.33 |
|
|
Monohydrogen phosphate |
HPO4-2 = H+ + PO4-3 |
12.3 |
|
|
Bisulfide ion |
HS- = H+ + S-2 |
13.9 |
|
|
Temperature °C |
DO saturation (Cs) in mg/L |
|
0 |
14.62 |
|
1 |
14.23 |
|
2 |
13.84 |
|
3 |
13.48 |
|
4 |
13.13 |
|
5 |
12.80 |
|
6 |
12.48 |
|
7 |
12.17 |
|
8 |
11.87 |
|
9 |
11.59 |
|
10 |
11.33 |
|
11 |
11.08 |
|
12 |
10.83 |
|
13 |
10.60 |
|
14 |
10.37 |
|
15 |
10.15 |
|
16 |
9.95 |
|
17 |
9.74 |
|
18 |
9.54 |
|
19 |
9.35 |
|
20 |
9.17 |
|
21 |
8.99 |
|
22 |
8.83 |
|
23 |
8.68 |
|
24 |
8.53 |
|
25 |
8.38 |
|
26 |
8.22 |
|
27 |
8.07 |
|
28 |
7.92 |
|
29 |
7.77 |
|
30 |
7.63 |
|
31 |
7.51 |
|
32 |
7.42 |
|
33 |
7.28 |
|
34 |
7.17 |
|
35 |
7.07 |
|
36 |
6.96 |
|
37 |
6.86 |
|
38 |
6.75 |
Use a θ (theta) of 1.135 for adjusting deoxygenation coefficients
Conversion factors: 1 gal = 3.7854x10-3 m3, 1 ft = 0.3048 m
Other Constants of interest: